Cho tam giác abc,be và cf là đg cao, m là tđ bc, h là giao điểm be và cf. Lấy k sao cho m là tđ hk
a) chứng minh bhck là hbh
b) chứng minh ab vg góc bk, ac vuông góc ck
c) lấy i sao cho bc là đường trung trực hi. Chứng minh bikc là hình thang cân
d) gọi g là giao điểm hi và bk, tìm đk của tam giác abc để chgk là hình thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Gọi giao của AH với BC là M
=>AH vuông góc BC tại M
góc AFH=góc AEH=90 độ
=>AEHF nội tiếp đường tròn đường kính AH
=>IF=IA=IE=IH
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>KF=KE=KB=KC
góc IFH+góc KFH
=góc IHF+góc KCH
=góc KCH+90 độ-góc KCH=90 độ
=>FK vuông góc FI
b: FI=AH/2=3cm
FK=BC/2=4cm
=>IK=căn 3^2+4^2=5cm

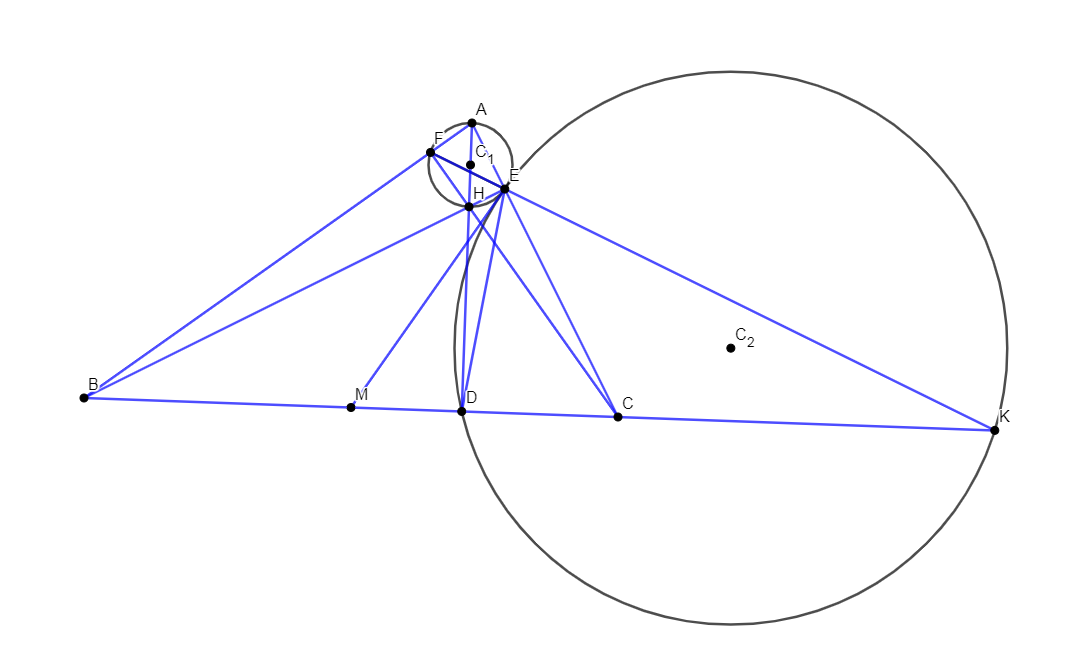
Có \(\Delta ECB\) vuông tại E và có EM là đường trung tuyến
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\)
\(\Rightarrow\Delta EBM\) cân tại M
\(\Rightarrow\widehat{BEM}=\widehat{MBE}\)
mà \(\widehat{MBE}=\widehat{CAD}\) (vì cùng phụ góc BCA)
\(\Rightarrow\widehat{BEM}=\widehat{CAD}\)
\(\Rightarrow\)EM là tiếp tuyến của (C1)
CM tương tự đc EM là tiếp tuyến của (C2)

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI

Ta cần chứng minh H là trực tâm của tam giác ASM. Với mục đích này, ta sẽ sử dụng tính chất của hình chữ nhật.
Vì M là trung điểm BC, ta có BM = MC. Do đó, SM là đường trung trực của BC.
Vì EF ⊥ BE và CF, nên EF song song với đường BC (vì BE // CF). Do đó, S nằm trên đường trung trực của BC.
Vì H là giao điểm của AD và BE, ta có AH ⊥ BC và BH ⊥ AC. Do đó, AH // SM và BH // SM.
Khi đó, ta suy ra được rằng tứ giác ABSH là hình chữ nhật (do có 2 cặp cạnh đối nhau là song song và bằng nhau).
Do AS là đường chéo của hình chữ nhật ABSH, nên H là trực tâm của tam giác ASM.
Vậy, H là trực tâm của tam giác ASM.
Bạn nhầm đề không vậy:), s là giao điểm cả ef và bc mà suy ra được s là trung trực của bc dc hả?:) nhân tài đất Việt đây rồi !! 🤣🤣🤣🤣🤣

a: Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>CK//AH
Xét (O) có
ΔBAK nội tiếp
BK là đường kính
Do đó: ΔBAK vuông tại A
=>AK//CH
Xét tứ giác CHAK có
CH//AK
CK//AH
DO đó: CHAK là hình bình hành
a: Xét tứ giác BHCK có
M là trung điểm chung của BC và HK
=>BHCK là hình bình hành
b: BHCK là hình bình hành
=>BH//CK và BK//CH
Ta có: BH//CK
BH\(\perp\)AC
Do đó: CK\(\perp\)CA
Ta có: BK//CH
AB\(\perp\)CH
Do đó; BK\(\perp\)BA
c: Gọi O là giao điểm của HI và BC
BC là đường trung trực của HI
=>BC\(\perp\)HI tại O và O là trung điểm của HI
Xét ΔHIK có
O,M lần lượt là trung điểm của HI,HK
=>OM là đường trung bình của ΔHIK
=>OM//IK
=>IK//BC
Xét ΔCHI có
CO là đường cao
CO là đường trung tuyến
Do đó: ΔCHI cân tại C
=>CH=CI
mà CH=BK
nên BK=CI
Xét tứ giác BCKI có
BC//KI
BK=CI
Do đó: BCKI là hình thang cân