với m=-1 vẽ (d1) (d2) trên cùng mptđ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
0
18 tháng 12 2016
a)( x= 0 ; y = 1); (y=0; x= 1/2) đt1
(x=0;y = -1) ; (y=0;x= 1) đt2
b) giao điểm tức là cùng nghiệm
-2x+1 = x- 1 => x = 2/3 ; y = -1/3
A(2/3; -1/3)
c) anh xem đk // là làm dc, em mệt r
11 tháng 12 2021
1: Để hai đường thẳng cắt nhau thì
2m+1<>m+2
hay m<>1
CM
20 tháng 4 2018
Với m = 2 thì d 1 : y = 2x + 3; d 2 : y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
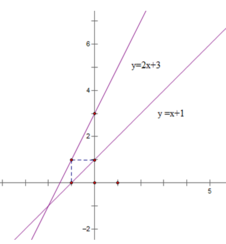
Gọi A ( x 0 ; y 0 ) là tọa độ giao điểm của d1 và d2
Khi đó:
( y 0 = 2 x 0 + 3 và y 0 = x 0 + 1
⇒ 2xo + 3 = x 0 + 1 ⇔ x 0 = -2
⇒ y 0 = x 0 + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của d 1 và d 2 là (-2; -1)
20 tháng 4 2023
a: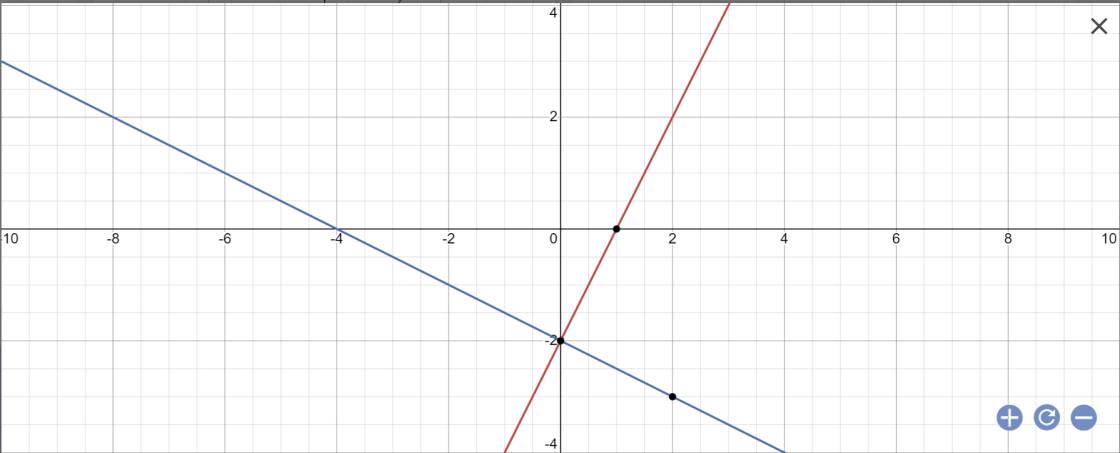 
b: Tọa độ A là:
2x-2=-1/2x-2 và y=2x-2
=>x=0 và y=-2
Tọa độ B là:
y=0 và 2x-2=0
=>x=1 và y=0
Tọa độ C là:
y=0 và -1/2x-2=0
=>x=-4; y=0
i: A(0;-2); B(1;0); C(-4;0)
\(\overrightarrow{AB}=\left(1;2\right);\overrightarrow{AC}=\left(-4;2\right)\)
Vì 1*(-4)+2*2=0
nên ΔABC vuông tại A
ii: \(AB=\sqrt{1^2+2^2}=\sqrt{5}\)
\(AC=\sqrt{\left(-4\right)^2+2^2}=2\sqrt{5}\)
\(BC=\sqrt{5+20}=5\left(cm\right)\)
\(C_{ABC}=AB+AC+BC=5+3\sqrt{5}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{5}=5\left(cm^2\right)\)
Câu trả lời hay nhất: -nhận xét:
d1: x-3y-2=0, điểm M(2;0) thuộc d1.
d2: x-3y+18=0
==> d1 // d2 , gọi C là đường tròn tâm I(a;b), bán kính R qua A(4;2) và tiếp xúc với d1, d2
==> I thuộc đường thẳng d nằm chính giữa và song song với d1, d2
==>d có phương trình: x-3y+(18-2)/2 =0 <==> x-3y+8=0
==> a-3b+8=0 <==> a= 3b-8 (1)
và 2R= k/c (d1,d2) = k/c ( M,d2) = [giá trị tuyệt đối của (2-3*0+18)]/[căn (1^2 + (-3)^2)]
==> 2R= 2 căn 10
==> R= căn 10 <==> R^2 = 10
*) AI= R <==> AI^2 = R^2 <==> (a-4)^2 + (b-2)^2 = 10 (2)
*) từ (1) và (2) ==> (3b-8-4)^2 + (b-2)^2 = 10
<==> (3b-12)^2 + (b-2)^2 = 10
<==> 10b^2 -76b + 138 =0
<==> b = 3 hoặc b = 23/5
+) b=3 ==> a= 3*3-8 =1
==> PT đường tròn: (x-1)^2 + (y-3)^2 =10
+) b= 23/5 ==> a= 3*23/5 -8 = 29/5
==> PT đường tròn: (x- 29/5)^2 + (y-23/5)^2 =10
good luck!
ok tk cho mk nha ^_^