cho tập A = [1;8] và B = { x thuộc R | x^2-2(m+1)+m+3 = 0 } . Có bao nhiêu giá trị nguyên của tham số m để thỏa mã điều kiện B có đúng hai tập con và B là con A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
31 tháng 3 2017
Đáp án A
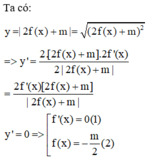
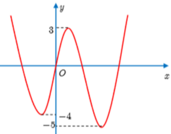
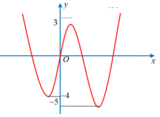
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy

CM
31 tháng 7 2018
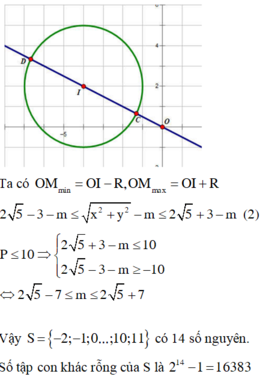
Chọn đáp án B.
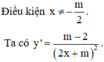
Hàm số đã cho đồng biến trên khoảng - ∞ ; - 8

Do đó, số tập con gồm 3 phần tử của tập hợp A là C 14 3 = 364



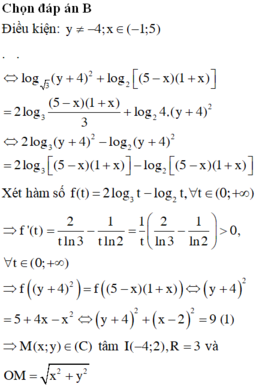
Gọi số phần tử của B là x
(Điều kiện: x∈\(N^{\star}\) )
Để B có đúng 2 tập con thì \(2^{x}=2\)
=>x=1
=>B có duy nhất 1 phần tử
\(x^2-2\left(m+1\right)x+m+3=0\) (1)
\(\Delta=\left\lbrack2\left(m+1\right)\right\rbrack^2-4\left(m+3\right)\)
\(=4\left(m+1\right)^2-4\left(m+3\right)\)
\(=4\left(m^2+2m+1-m-3\right)=4\left(m^2+m-2\right)\)
=4(m+2)(m-1)
Để B có 1 phần tử duy nhất thì phương trình (1) có duy nhất 1 nghiệm
=>Δ=0
=>(m+2)(m-1)=0
=>\(\left[\begin{array}{l}m+2=0\\ m-1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}m=-2\\ m=1\end{array}\right.\)
Khi m=-2 thì (1) sẽ trở thành:
\(x^2-2\left(-2+1\right)x+\left(-2\right)+3=0\)
=>\(x^2+2x+1=0\)
\(\) =>\(\left(x+1\right)^2=0\)
=>x+1=0
=>x=-1
mà -1 không thuộc [1;8]
nên Loại
Khi m=1 thì (1) sẽ trở thành:
\(x^2-2\left(1+1\right)x+1+3=0\)
=>\(x^2-4x+4=0\)
=>\(\left(x-2\right)^2=0\)
=>x-2=0
=>x=2∈[1;8]
=>Nhận
=>m=1 là giá trị m nguyên duy nhất thỏa mãn yêu cầu đề bài
=>Có 1 giá trị m thỏa mãn