Cho đường tròn (O) và hai dây MA, MB vuông góc với nhau. Gọi I, K lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm của AK và BI. Chứng minh :
a) ba điểm A, O, B thẳng hàng
b) P là tâm đường tròn nội tiếp tam giác MAB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

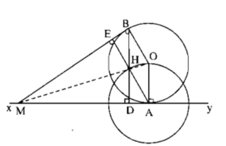
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO

Answer:
a, \(\Delta MAB\) nội tiếp \(\left(O\right)\) có \(\widehat{AMB}=90^o\)
\(\Rightarrow AB\) là đường kính \(\left(O\right)\)
\(\Rightarrow AB\) đi qia tâm O của đường tròn
Vậy ba điểm A, O, B thẳng hàng
b, Vì I là điểm chính giữa cung nhỏ MA
\(\Rightarrow\widebat{IA}=\widebat{IM}\)
\(\Rightarrow\widehat{ABI}=\widehat{MBI}\)
\(\Rightarrow IB\) là tia phân giác của \(\widehat{MBA}\)
Vì K là điểm chính giữa cung nhỏ MB
\(\Rightarrow\widebat{KB}=\widebat{KM}\)
\(\Rightarrow\widehat{BAK}=\widehat{MAK}\)
\(\Rightarrow AK\) là tia phân giác của \(\widehat{MAK}\)
\(\Delta MAB\) có hai đường phân giác AK và IB cắt nhau tại P
Vậy P là đường tròn nội tiếp \(\Delta MAB\)

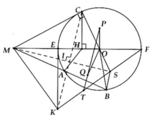
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng

A B C H M N
a, Vì HM là đường cao => \(HM\perp AB\)=> ^HMA = 900
Vì HN là đường cao => \(HN\perp AC\)=> ^HNA = 900
Xét tứ giác AMHN có :
^HMA + ^HNA = 900
mà ^HMA ; ^HNA đối nhau
Vậy tứ giác AMHN nội tiếp
b, Xét tam giác ABH vuông tại H, đường cao HM ta có :
\(AH^2=AM.AB\)(1)
Xét tam giác ACH vuông tại H, đường cao HN ta có :
\(AH^2=AN.AC\)(2)
từ (1) ; (2) suy ra : \(AM.AB=AN.AC\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\)
Xét tam giác AMN và tam giác ACB ta có :
^A chung
\(\frac{AM}{AC}=\frac{AN}{AB}\)( cmt )
Vậy tam giác AMN ~ tam giác ACB ( c.g.c )
a) Do MA ⊥ MB (gt)
⇒ ∠MAB = 90⁰
⇒ M, A, B thuộc đường tròn đường kính AB
Mà M, A, B thuộc (O)
⇒ O là trung điểm của AB
⇒ A, O, B thẳng hàng
b) Do I là điểm chính giữa của cung nhỏ MA (gt)
⇒ sđ cung AI = sđ cung MI
⇒ ∠ABI = ∠MBI (hai góc nội tiếp chắn hai cung bằng nhau)
⇒ BI là tia phân giác của ∠ABM
Do K là điểm chính giữa của cung MB (gt)
⇒ sđ cung BK = sđ cung MK
⇒ ∠BAK = ∠MAK (hai góc nội tiếp chắn hai cung bằng nhau)
⇒ AK là tia phân giác của ∠BAM
Mà P là giao điểm của AK và BI (gt)
⇒ P là giao điểm của ba đường phân giác của ∆MAB
⇒ P là tâm đường tròn nội tiếp ∆MAB
a.
Do \(OM=OA=R\Rightarrow\Delta OAM\) cân tại O
\(\Rightarrow\widehat{OAM}=\widehat{OMA}\Rightarrow\widehat{AOM}=180^0-\left(\widehat{OAM}+\widehat{OMA}\right)=180^0-2\widehat{OMA}\)
Tương tự, \(\Delta OBM\) cân tại O
\(\Rightarrow\widehat{BOM}=180^0-2\widehat{OMB}\)
\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2\left(\widehat{OMA}+\widehat{OMB}\right)\)
\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2.\widehat{AMB}=360^0-2.90^0=180^0\)
\(\Rightarrow A,O,B\) thẳng hàng
b.
Do I là điểm chính giữa cung MA \(\Rightarrow sđ\stackrel\frown{AI}=sđ\stackrel\frown{MI}\Rightarrow\widehat{ABI}=\widehat{MBI}\)
\(\Rightarrow BI\) là tia phân giác góc \(\widehat{ABM}\) (1)
Do K là điểm chính giữa cung MB \(\Rightarrow sđ\stackrel\frown{MK}=sđ\stackrel\frown{BK}\Rightarrow\widehat{MAK}=\widehat{BAK}\)
\(\Rightarrow AK\) là tia phân giác góc \(\widehat{MAB}\) (2)
(1);(2) \(\Rightarrow P\) là giao điểm 2 đường phân giác trong của tam giác MAB
\(\Rightarrow P\) là tâm đường tròn nội tiếp tam giác MAB