Cho tam giác ABC có góc A < 90 độ . Trên nữa mặt phẳng bờ AB ko chứa C , vẽ tia Ax vuông góc AB , trên đó lấy D sao cho AD= AB .Trên nửa mặt phẳng bờ AC ko chứa B , vẽ tia Ay vuông góc AC . Trên đó lấy E sao cho AE=AC
a) CM : tam giác ACD = tam giác AEB
b)CM : EB vuông góc CD
c) các đường thẳng ED và AC có vuông góc với nhau ko? Vì sao
có anh chị nào onl ko giúp em nhanh với

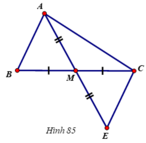
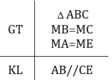
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có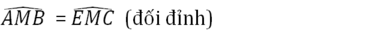

A B C D E K I
a/
Ta có
AD=AB (gt) (1); AC=AE (gt) (2)
\(\widehat{CAD}=\widehat{BAD}+\widehat{A}=90^o+\widehat{A}\)
\(\widehat{BAE}=\widehat{CAE}+\widehat{A}=90^o+\widehat{A}\)
\(\Rightarrow\widehat{CAD}=\widehat{BAE}\) (3)
Từ (1) (2) (3) => tg ACD = tg AEB (c.g.c)
b/
Gọi K là giao của CD và AB; I là giao của CD và BE
tg ACD = tg AEB (cmt) \(\Rightarrow\widehat{ADC}=\widehat{ABE}\) (4)
\(\widehat{AKD}=\widehat{IKB}\) (góc đối đỉnh) (5)
Xét tg vuông ADK có
\(\widehat{ADC}+\widehat{AKD}=90^o\) (6)
Từ (4) (5) (6) \(\Rightarrow\widehat{ABE}+\widehat{IKB}=90^o\)
Xét tg BIK có
\(\widehat{ABE}+\widehat{IKB}=90^o\) (cmt) \(\Rightarrow\widehat{BIK}=90^o\Rightarrow EB\perp CD\)
c/
Ta có \(AE\perp AC\left(gt\right)\) => ED không thể vuông góc với AC được (Từ 1 điểm ở ngoài 1 đưởng thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho)
Giải:
a; Theo bài ra ta có hình h1
Xét \(\Delta\)ACD và \(\Delta\)AEB có:
AD = AB(gt)
AC = AE (gt)
\(\widehat{DAC}\) = 900 + \(\widehat{BAC}\)
\(\widehat{BAE}\) = 900 + \(\widehat{BAC}\)
⇒ \(\widehat{DAC}\) = \(\widehat{BAE}\)
Vậy \(\Delta\)ACD = \(\Delta\)AEB (c-g-c)
b; Gọi J, K lần lượt là giao điểm của BE và DC; BE và AC
khi đó: \(\widehat{AKE}\) = \(\widehat{CKJ}\) (vì đối đỉnh)
\(\Delta\)ACD = \(\Delta\)AEB (cmt)
⇒ \(\widehat{AEK}\) = \(\widehat{AEB}\) = \(\widehat{ACD}\) = \(\widehat{KCJ}\)
⇒ \(\widehat{AKE}\) + \(\widehat{AEK}\) = \(\widehat{CKJ}\) + \(\widehat{KCJ}\)
Mặt khác ta có:
\(\widehat{AKE}\) + \(\widehat{AEK}\) + \(\widehat{EAK}\) = 1800 (tổng ba góc trong một tam giác)
\(\widehat{EAK}\) = 900 vì AE \(\perp\) AC theo gt
⇒ \(\widehat{AKE}\) + \(\widehat{AEK}\) = 1800 - 900 = 900
⇒ \(\widehat{CKJ}\) + \(\widehat{KCJ}\) = 900
\(\widehat{BJC}\) = \(\widehat{CKJ}\) + \(\widehat{KCJ}\) = 900 (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
⇒ BE \(\perp\) CD
c; Kéo dài AC cắt DE tại F
Xét tam giác AEF ta có:
\(\widehat{DFA}\) = \(\widehat{FAE}\) + \(\widehat{AEF}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{FAE}\) = 900 (AE \(\perp\) AC theo gt)
⇒ \(\widehat{DFA}\) = 900 + \(\widehat{AEF}\) > 900
Vậy ED không vuông góc với AC