\(\left(x+\dfrac{1}{3}\right)^3=\left(\dfrac{2}{3}\right)^6\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 10 2023
a, \(x^2\) - 19 = 5.9
\(x^2\) - 19 = 45
\(x^2\) = 45 + 19
\(x^2\) = 64
\(x^2\) = 82
\(x\) = 8
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 10 2023
b, (2\(x\) + 1)3 = -0,001
(2\(x\) + 1)3 = (-0,1)3
2\(x\) + 1 = -0,1
2\(x\) = -0,1 - 1
2\(x\) = - 1,1
\(x\) = -1,1: 2
\(x\) = - 0,55
29 tháng 10 2021
3: \(\left|x-\dfrac{3}{4}\right|-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left|x-\dfrac{3}{4}\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{4}=\dfrac{1}{2}\\x-\dfrac{3}{4}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{1}{4}\end{matrix}\right.\)
20 tháng 1 2022
Câu 1:
=>15(2x+1)-8(3x-1)=100
=>30x+15-24x+8=100
=>6x+23=100
hay x=77/6
Câu 2:
=>2(5x-3)+12-3(7x-1)=x+2
=>10x-6+12-21x+3-x-2=0
=>-12x=-7
hay x=7/12
Câu 3:
\(\Leftrightarrow2\left(x^2-1\right)+3\left(x+1\right)=2\left(x^2-4x+4\right)\)
\(\Leftrightarrow2x^2-2+3x+3-2x^2+8x-8=0\)
=>11x-7=0
hay x=-7/11
20 tháng 1 2022
Câu 4:
(x - 4)^3/6 + 1 = x(x + 1)/2 - (x - 5)(x + 5)/3
<=> (x - 4)^3 + 6/6 = x^2 + x/2 - x^2 - 25/3
<=> (x - 4)^3 + 6/6 = 3x^2 + 3x - 2x^2 + 50/6
<=> (x - 4)^3 + 6 = 3x^2 + 3x - 2x^2 + 50
<=> x^3 - 12x^2 + 48x - 58 = x^2 + 3x + 50
<=> x^3 -13x^2 + 45x - 108 = 0
Đến đây bạn bấm máy nhẩm nghiệm là ra nhé
Câu 5:
3(x + 2)^3/5 - (x - 1)^2/10 = (x - 3)(x + 3)/2
<=> 6(x + 2)^3 - (x - 1)^2/10 = 5(x^2 - 9)/10
<=> 6(x + 2)^3 - (x - 1)^2 = 5(x^2 - 9)
<=> 6x^3 + 36x^2 + 72x + 48 - x^2 + 2x - 1 - 5x^2 + 45 = 0
<=> 6x^3 + 30x^2 + 74x + 92 = 0
Đến đây bạn bấm máy nhẩm nghiệm như câu 4 nhé
28 tháng 1 2022
\(1,\) thiếu đề
\(2,\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)
\(\Leftrightarrow\dfrac{5\left(5x+2\right)}{30}-\dfrac{10\left(8x-1\right)}{30}=\dfrac{6\left(4x+2\right)}{30}-\dfrac{150}{30}\)
\(\Leftrightarrow5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)
\(\Leftrightarrow25x+10-80x+10=24x+12-150\)
\(\Leftrightarrow-55x+20=24x-138\)
\(\Leftrightarrow24x-138+55x-20=0\)
\(\Leftrightarrow79x-158=0\)
\(\Leftrightarrow x=2\)
\(3,ĐKXĐ:\left\{{}\begin{matrix}x\ne1\\x\ne-1\\x\ne3\end{matrix}\right.\\ \dfrac{x}{2x-6}+\dfrac{x}{2x-2}=\dfrac{-2x}{\left(x+1\right)\left(3-x\right)}\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(3-x\right)}=0\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}-\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=0\)
\(\Leftrightarrow x\left(\dfrac{1}{2\left(x-3\right)}+\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{\left(x+1\right)\left(x-3\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4\left(x-1\right)}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{x^2-1}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{x^2-2x-3}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4x-4}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x.\dfrac{x^2-1+x^2-2x-3-4x+4}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x^2-6x}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x\left(x-3\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{x}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x=0\)
14 tháng 4 2023
a: =>11(x-3)=6(x-5)
=>11x-33=6x-30
=>5x=3
=>x=3/5
b: =>(4/3-1/4x-5/12)-2x=8/5*5/3=8/3
=>-9/4x+11/12=8/3
=>-9/4x=32/12-11/12=21/12=7/4
=>x=-7/9
c: =>1/2x-1/3-2/3x-1=x
=>-1/6x-4/3=x
=>-7/6x=4/3
=>x=-4/3:7/6=-4/3*6/7=-24/21=-8/7
d: =>1-2x-3x+1=7/2
=>-5x=3/2
=>x=-3/10
MH
19 tháng 2 2022
1) \(\left(x-2\right)\left(3+2x\right)-2x\left(x+5\right)=6\)
\(3x+2x^2-6-4x-2x^2-10x-6=0\)
\(-11x=12\)
\(x=-\dfrac{12}{11}\)
2) \(x^2-4-\left(x-5\right)\left(x-2\right)=0\)
\(\left(x-2\right)\left(x+2\right)-\left(x-5\right)\left(x-2\right)=0\)
\(\left(x-2\right)\left(x+2-x+5\right)=0\)
\(7\left(x-2\right)=0\)
\(\Leftrightarrow x=2\)
19 tháng 2 2022
1, \(3x+2x^2-6-4x-2x^2-10x=0\Leftrightarrow-11x-6=0\Leftrightarrow x=-\dfrac{6}{11}\)
2, \(\left(x-2\right)\left(x+2\right)-\left(x-5\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-x+5\right)=0\Leftrightarrow x=2\)
3, bạn xem lại đề
5, đk x khác -4 ; 4
\(96=\left(2x-1\right)\left(x-4\right)+\left(3x-1\right)\left(x+4\right)-6\left(x^2-16\right)\)
\(\Leftrightarrow96=2x^2-9x+4+3x^2+11x-4-6x^2+96\)
\(\Leftrightarrow-x^2+2x=0\Leftrightarrow-x\left(x-2\right)=0\Leftrightarrow x=0;x=2\)(tm)
22 tháng 3 2021
ĐKXĐ: \(x\notin\left\{-1;-2;-3;-4\right\}\)
Ta có: \(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{x+4}{\left(x+1\right)\left(x+4\right)}-\dfrac{x+1}{\left(x+1\right)\left(x+4\right)}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{x^2+5x+4}{6\left(x+1\right)\left(x+4\right)}\)
\(\Leftrightarrow\dfrac{18}{6\left(x+1\right)\left(x+4\right)}=\dfrac{x^2+5x+4}{6\left(x+1\right)\left(x+4\right)}\)
Suy ra: \(x^2+5x+4=18\)
\(\Leftrightarrow x^2+5x-14=0\)
\(\Leftrightarrow x^2+7x-2x-14=0\)
\(\Leftrightarrow x\left(x+7\right)-2\left(x+7\right)=0\)
\(\Leftrightarrow\left(x+7\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+7=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-7;2}
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
27 tháng 1
\(Đặt:\left\{{}\begin{matrix}a=\dfrac{1}{\left|x+3\right|}\left(ĐK:x\ne-3\right)\\b=\dfrac{1}{\left|y\right|-2}\left(ĐK:y\ne\pm2\right)\end{matrix}\right.\\ Có:\left\{{}\begin{matrix}\dfrac{1}{\left|x+3\right|}+\dfrac{4}{\left|y\right|-2}=\dfrac{11}{6}\\\dfrac{5}{\left|x+3\right|}+\dfrac{2}{\left|y\right|-2}=\dfrac{11}{6}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a+4b=\dfrac{11}{6}\\5a+2b=\dfrac{11}{6}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a+4b=\dfrac{11}{6}\\10a+4b=\dfrac{22}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-9a=-\dfrac{11}{6}\\a+4b=\dfrac{11}{6}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{11}{54}\\b=\dfrac{\dfrac{11}{6}-\dfrac{11}{54}}{4}=\dfrac{11}{27}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{\left|x+3\right|}=a=\dfrac{11}{54}\\\dfrac{1}{\left|y\right|-2}=b=\dfrac{11}{27}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11\left|x+3\right|=54\\11\left(\left|y\right|-2\right)=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|x+3\right|=\dfrac{54}{11}\\\left|y\right|=\dfrac{27}{11}+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x+3=\dfrac{54}{11}\\x+3=\dfrac{-54}{11}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{27}{11}+2\\y=-\left(\dfrac{27}{11}+2\right)\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\dfrac{21}{11}\left(TM\right)\\x=\dfrac{-87}{11}\left(TM\right)\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{49}{11}\left(TM\right)\\y=-\dfrac{49}{11}\left(TM\right)\end{matrix}\right.\end{matrix}\right.\\ Vậy:\left(x;y\right)=\left\{\left(\dfrac{21}{11};\dfrac{49}{11}\right);\left(\dfrac{-87}{11};\dfrac{49}{11}\right);\left(\dfrac{21}{11};\dfrac{-49}{11}\right);\left(\dfrac{-87}{11};\dfrac{-49}{11}\right)\right\}\)
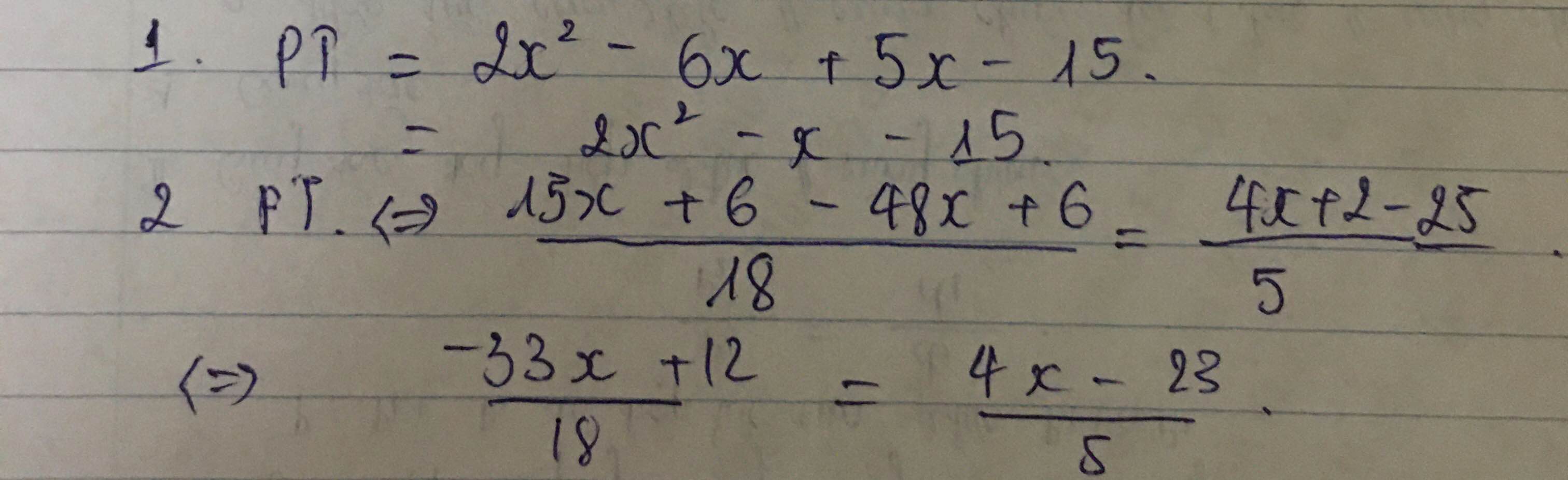
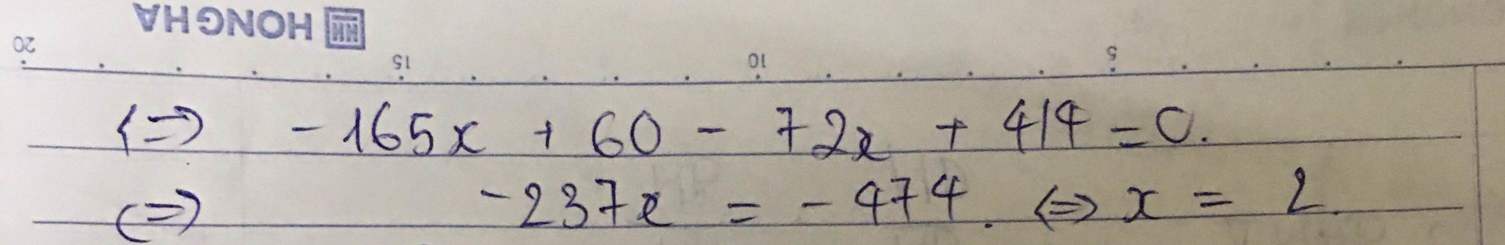
\(\left(x+\dfrac{1}{3}\right)^3=\left(\dfrac{2}{3}\right)^6\\ \Rightarrow\left(x+\dfrac{1}{3}\right)^3=\left[\left(\dfrac{2}{3}\right)^2\right]^3\\ \Rightarrow\left(x+\dfrac{1}{3}\right)^3=\left(\dfrac{4}{9}\right)^3\\ \Rightarrow x+\dfrac{1}{3}=\dfrac{4}{9}\\ \Rightarrow x=\dfrac{4}{9}-\dfrac{1}{3}\\ \Rightarrow x=\dfrac{4}{9}-\dfrac{3}{9}\\ \Rightarrow x=\dfrac{1}{9}\)