Rút gọn
A= sin( x-9π/2).tan(x+7π) - cos(x-7π/2)
(MONG DC M.N GIÚP Ạ EM CẢM ƠN RẤT NHIỀU!!😢😢)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 8 2018
B1:
a,\(\left(3x-2\right)\left(x-3\right)=3x^2-9x-2x+6=3x^2-11x+6\)
b,\(\left(2x+1\right)\left(x+3\right)=2x^2+6x+x+3=2x^2+7x+3\)
c,\(\left(x-3\right)\left(3x-1\right)=3x^2-x-9x+3=3x^2-10x+3\)
B2:
1)\(x^2-\left(x+4\right)\left(x-1\right)=x^2-\left(x^2-x+4x-4\right)=x^2-x^2+x-4x+4=-3x+4\)
2)\(x\left(x+2\right)-\left(x-2\right)\left(x+4\right)=x^2+2x-\left(x^2+4x-2x-8\right)\)
\(=x^2+2x-x^2-4x+2x+8=8\)
24 tháng 8 2018
4) (3x-2)(x-3)= 3x(x-3)-2(x-3)
=3x.x+3x.(-3)-2.x-2.(-3)
=\(3x^2\)-9x-4x+6
=\(3x^2\)+(-9x-4x)+6
=\(3x^2\)-13x+6
5) (2x+1)(x+3)=2x(x+3)+1(x+3)
=2x.x+2x.3+1.x+1.3
=\(2x^2\)+6x+1x+3
=\(2x^2\)+(6x+1x)+3
=\(2x^2\)+7x+3
6) (x-3)(3x-1)=x(3x-1)-3(3x-1)
=x.3x+x.(-1)-3.3x-3.(-1)
=\(3x^2\)-1x-9x+3
=\(3x^2\)+(-1x-9x)+3
=\(3x^2\)-10x+3
rút gọn biểu thức
A) \(x^2\)-(x+4)(x-1)=\(x^2\)- x(x-1)-4(x-1)
=\(x^2\)-x.x-x.(-1)-4.x-4.(-1)
=\(x^2\)-\(x^2\)+1x-4x+4
=(\(x^2-x^2\))+(1x-4x)+4
= -3x+4
B) x(x+2)-(x-2)(x+4)=x.x+x.2-x(x+4)+2(x+4)
=\(x^2+2x\)-x.x-x.4+2.x+2.4
=\(x^2+2x-x^2-4x+2x+8\)
=(\(x^2-x^2\))+(2x-4x+2x)+8
=8
tính giá trị biểu thức
A=3(x-2)-(2+x)(x-3)
=3.x+3.(-2)-2(x-3)-x(x-3)
=3x-6-2.x-2.(-3)-x.x-x(-3)
=3x-6-2x+6-\(x^2\)+3x
=(3x-2x+3x)+(-6+6)\(-x^2\)
=4x - \(x^2\)
thay x=-8 vào biểu thức thu gọn ta được:
4.(-8)- (-8)\(^2\)
= - 32 +64
= 32
B= x(3-x)-(1+x)(1-x)
=x.3+x.(-x)-1(1-x)-x(1-x)
=3x -\(x^2\)-1.1-1 .(-x)-x.1-x.(-x)
=3x\(-x^2\)-\(1^2\)+1x-1x+\(x^2\)
=(3x+1x-1x)+(\(-x^2+x^2\))-1
=3x-1
thay x=-5 vào biểu thức thu gọn ta được:
3.(-5)-1
=-15-1
=-16
24 tháng 8 2018
Thu gọn biểu thức
4) (3x - 2) (x - 3)
= ( 3x2 - 2x ) - ( 3x x 3 - 2 x 3 )
= 3x2 - 2x - 3x x 3 + 2 x 3
= 3x2 - 2x - 9x + 6
= 3x2 - 11x + 6
5) (2x + 1) (x + 3)
= ( 2x2 + 1x ) + ( 6x + 3 )
= 2x2 + 1x + 6x + 3
= 2x2 + 7x + 3
6) (x - 3) (3x - 1)
= ( 3x2 - 9x ) - ( x - 3 )
= 3x2 - 9x - x + 3
= 3x2 - 10 + 3
Rút gọn biểu thức
A) x^2 - (x + 4) (x - 1)
= x2 - ( x2 + 4x ) - ( x + 4 )
= x2 - x2 - 4x - x - 4
= -5x - 4
B) x (x + 2) - (x - 2) (x + 4)
= x2 + 2x - ( x2 - 2x ) + ( 4x - 8 )
= x2 + 2x - x2 + 2x + 4x - 8
= 8x - 8
Tính giá trị biểu thức
A = 3 (x - 2) - (2 + x) (x - 3) tại x = - 8
Thế x = -8 vào, ta có :
= 3 ( -8 -2 ) - ( 2 + -8 ) ( -8 - 3 )
= 3 x ( -10 ) - ( - 6 ) ( -11 )
= -30 - 66
= -96
B = x (3 - x) - (1 + x) ( 1 - x) tại x = - 5
Thế x = - 5 vào, ta có :
= -5 ( 3 - -5 ) - ( 1+ -5 ) ( 1 - -5 )
= -5 x 8 - (-4) x 6
= - 40 - -24
= -40 + 24
= -16
100% đúng
hok tốt nha
6 tháng 7 2019
a) Ta có: \(\sin^2a^o=\cos^2\left(90^o-a^o\right)\)
Biểu thức trên
\(=\left(\sin^21^o+\sin^o89\right)+\left(\sin^22^o+\sin^288^o\right)+...+\left(\sin^244^o+\sin^246^o\right)+\sin^245^o\)
\(=\left(\sin^21^o+\cos^21^o\right)+\left(\sin^22^o+\cos^22^o\right)+...+\left(\sin^244^o+\cos^246^o\right)+\sin^245^o\)
\(=1+1+..+1+\sin^245^o=44+\frac{1}{2}=\frac{89}{2}\)
b)
Ta có: \(\sin^2x+\cos^2x=1\)
\(0^o< x< 90^o\)
=> \(0< \sin x;\cos x< 1\)
Ta có: \(\frac{\sin^2x+\cos^2x}{\text{}\text{}\sin x.\cos x}=\frac{1}{\frac{12}{25}}=\frac{25}{12}\Leftrightarrow\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}=\frac{25}{12}\)
\(\Leftrightarrow\tan x+\frac{1}{\tan x}=\frac{25}{12}\Leftrightarrow\tan^2x-\frac{25}{12}\tan x+1=0\)
Đặt t =tan x => có phương trình bậc 2 ẩn t => Giải đen ta => ra đc t => ra đc tan t
\(\Leftrightarrow\orbr{\begin{cases}\tan x=\frac{3}{4}\\\tan x=\frac{4}{3}\end{cases}}\)
MH
0
PP
0
TC
7 tháng 2 2020
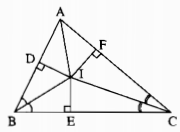
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
H
7 tháng 2 2020
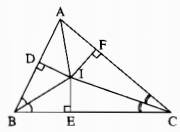
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W
\(A=sin\left(x-\dfrac{9\Omega}{2}\right)\cdot tan\left(x+7\Omega\right)-cos\left(x-\dfrac{7}{2}\Omega\right)\)
\(=sin\left(x-\dfrac{8}{2}\Omega-\dfrac{\Omega}{2}\right)\cdot tan\left(x+6\Omega+\Omega\right)-cos\left(x-\dfrac{8}{2}\Omega+\dfrac{\Omega}{2}\right)\)
\(=sin\left(x-\dfrac{\Omega}{2}\right)\cdot tan\left(x+\Omega\right)-cos\left(x+\dfrac{\Omega}{2}\right)\)
\(=-sin\left(\dfrac{\Omega}{2}-x\right)\cdot tanx-\left(-sinx\right)\)
\(=-cosx\cdot tanx+sinx=-sinx+sinx=0\)
😰🍚🍚🍚