K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2023
góc AIB<90 độ
=>góc BIC>90 độ
Xét ΔBIC có góc BIC>90 độ
nên BC là cạnh lớn nhất
=>BC>BI
CM
13 tháng 4 2019
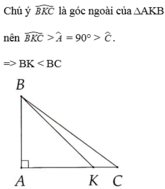
Trong ΔABK, ta có ∠BKC là góc ngoài tại đỉnh K nên ∠BKC = ∠A + ∠ABK
Suy ra: ∠BKC > ∠A = 90o (tính chất góc ngoài)
Trong ΔBKC ta có ∠BKC là góc tù, BC là cạnh đối diện với ∠BKC
Suy ra BC là cạnh lớn nhất
Do đó BC > BK.
2 tháng 3 2018
vì tam giác ABC là tam giác vuông tại A
⇒góc A=900
Xét tam giác ABK có
góc A = 900⇒góc A>góc BKA⇒BK > AB
có góc BKC = góc ABK+ góc A (BKC là góc ngoài của tam giác ABD)
⇒góc BKC > góc A⇒góc BKC>900
Xét tam giác BKC có:BKC>900 ⇒BKC > C
⇒BC>BK(quan hệ giữa cạnh và góc đối diện trong 1 tam giác)
vậy BC>BK
28 tháng 2 2023
góc AMB<90 độ
=>góc NMB>90 độ
=>BM<BN
góc ANB<90 độ
=>góc BNC>90 độ
=>BN<BC
=>BM<BN<BC
10 tháng 3 2016
Tam giác ABC vuông tại A.
=> A^ > C^ (1)
Ta lại có : ^CKB là góc ngoài tại đỉnh K của tam giác ABK
^CKB > ^A (2)
Từ (1) và (2) : => ^CKB > ^C
Tam giác BKC có : ^CKB > ^C
=> BC > BK ( quan hệ giữa góc và cạnh đối diện ).
k cko mình mình k lại cho..
15 tháng 7 2019
e nằm giữa A và C nên AE< AC \(\Rightarrow\)BE<BC( đường xiên nào có hình chiếu lớn hơn thì lớn hơn)
do tam giác ABC vuông tại A nên BA là đường vuông góc nên BA là đường thẳng ngắn nhất \(\Rightarrow\)BA<BE
Vậy BA<BE<BC
làm tương tự phần b
1 tháng 4 2020
Bài 1 bạn tự làm nhé
Bài 2 :
A A A B B B F F F C C C D D D E E E
Xét \(\Delta\)ADE vuông tại E :
AE < AD (1)
Xét \(\Delta\)CDF vuông tại F
CF < CD (2)
Từ (1) và (2) => AE + CF < AD + CD = AC
Bài 3 :
C C C B B B A A A N N N M M M H H H
Ta có : \(BM=BC\)=> \(\Delta\)BMC cân ở C nên \(\widehat{MCB}=\widehat{CMB}\)
Ta lại có : \(\widehat{BCM}+\widehat{MCA}=90^0,\widehat{CMH}+\widehat{MCH}=90^0\)
=> \(\widehat{MCH}=\widehat{MCN}\)
Xét \(\Delta\)MHC và \(\Delta\)MNC có :
MC chung
HC = NC(gt)
\(\widehat{MCH}=\widehat{MCN}\)(cmt)
=> \(\Delta\)MHC = \(\Delta\)MNC(c.g.c)
Do đó \(\widehat{MNC}=\widehat{MHC}=90^0\)
hay MN \(\perp\)AC
Ta có : BM = BC,CH = CN và AM > AN
Do đó BM + MA + CH > BC + CN + NA hay AB + CH > BC + CA
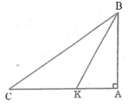
Do ABC vuông tại A \(\Rightarrow\widehat{C}< \widehat{A}\) (1)
Mặt khác theo tính chất góc ngoài của tam giác:
\(\widehat{BMC}=\widehat{A}+\widehat{ABM}\Rightarrow\widehat{BMC}>\widehat{A}\) (2)
(1);(2) \(\Rightarrow\widehat{BMC}>\widehat{C}\)
\(\Rightarrow BC>BM\)