Chứng minh rằng : \(\left(n+2005^{2006}\right)\left(n+2006^{2005}\right)\forall n\in N\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(VT=\frac{2\left(\sqrt{2}-\sqrt{1}\right)}{3.\left(2-1\right)}+\frac{2\left(\sqrt{3}-\sqrt{2}\right)}{5\left(3-2\right)}+...+\frac{2\left(\sqrt{2006}-\sqrt{2005}\right)}{4011\left(2006-2005\right)}\)
\(VT=\frac{2\left(\sqrt{2}-\sqrt{1}\right)}{3}+\frac{2\left(\sqrt{3}-\sqrt{2}\right)}{5}+...+\frac{2\left(\sqrt{2006}-\sqrt{2005}\right)}{4011}\)
Nhận xét: (a-b)2 \(\ge\) 0 => a2 + b2 \(\ge\) 2ab
Áp dụng ta có: \(3=\left(\sqrt{2}\right)^2+\left(\sqrt{1}\right)^2\ge2.\sqrt{2}.\sqrt{1}\)
\(5=\left(\sqrt{3}\right)^2+\left(\sqrt{2}\right)^2\ge2.\sqrt{3}.\sqrt{2}\)
...
\(4011=\left(\sqrt{2006}\right)^2+\left(\sqrt{2005}\right)^2\ge2.\sqrt{2006}.\sqrt{2005}\)
=> \(VT<\frac{2\left(\sqrt{2}-\sqrt{1}\right)}{2.\sqrt{2}.\sqrt{1}}+\frac{2\left(\sqrt{3}-\sqrt{2}\right)}{2.\sqrt{3}.\sqrt{2}}+...+\frac{2\left(\sqrt{2006}-\sqrt{2005}\right)}{2.\sqrt{2006}.\sqrt{2005}}\)
=> \(VT<1-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}...+\frac{1}{\sqrt{2005}}-\frac{1}{\sqrt{2006}}=1-\frac{1}{\sqrt{2006}}\)
=> điều phải chứng minh

Đúng là câu b sai, nhầm dấu đoạn đầu, phải là \(\frac{2006.2006-\left(2005.2006+2005\right)}{2006.\left(2007-2005\right)}\)
Phá ngoặc thì thành trừ nhưng cô của em bạn lại sót=> sai luôn cả tính chất bài toán.
P/s: Thử lại bằng casio là thấy rõ bạn đúng.
Tư tưởng bảo thủ của bọn trẻ con và niềm tin mù quáng vào thầy cô đó bạn ^^

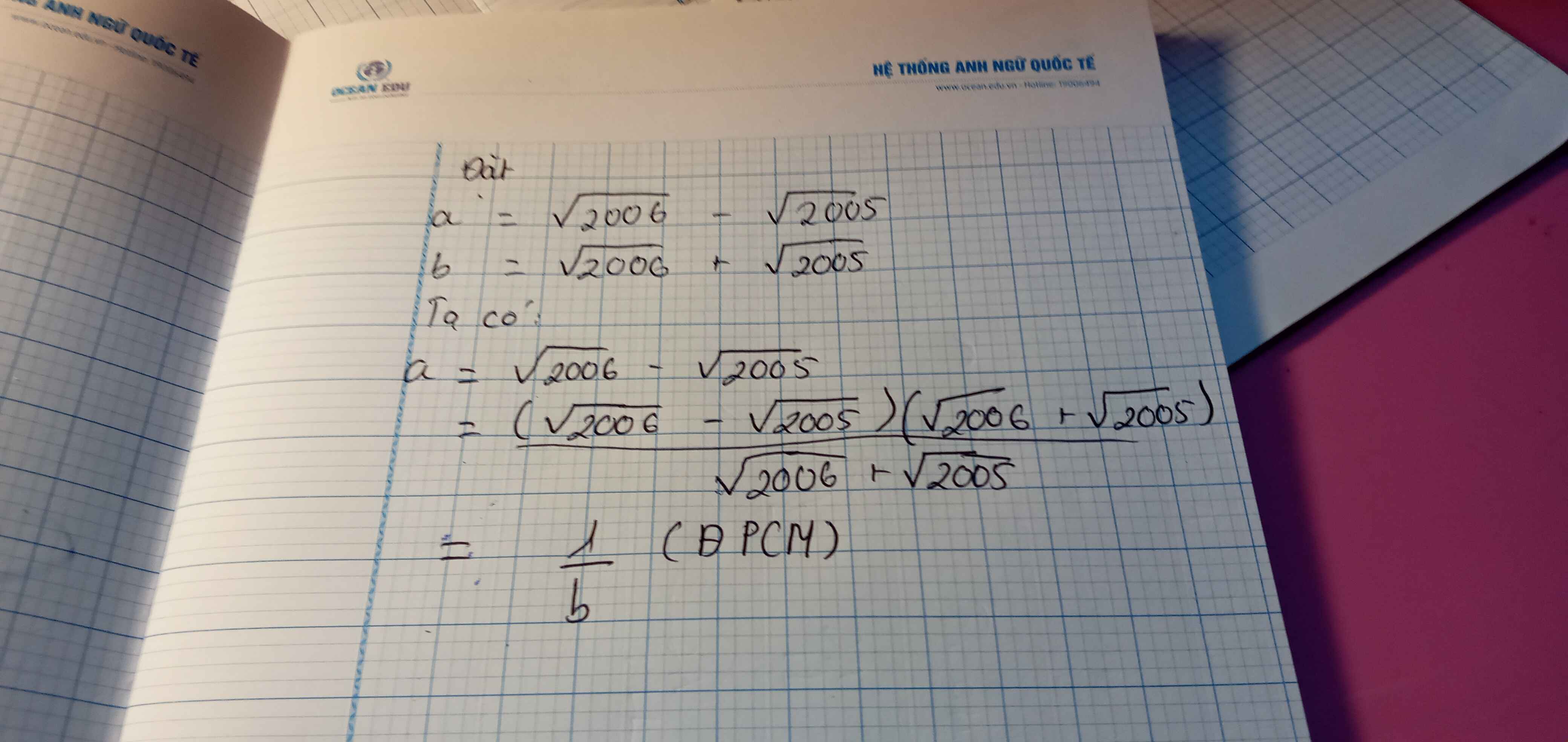
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)

Ta có a+b+c=0\(\Rightarrow\)\(\left(a+b+c\right)^2=0\)\(\Rightarrow a^2+b^2+c^2+2ab+2bc+2ca=0\)\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\)\(\Rightarrow a^2+b^2+c^2=0\).Mặt khác ta có :\(a^2\ge0\forall a;b^2\ge0\forall b;c^2\ge0\forall c\)\(\Rightarrow a=b=c=0\)\(\Rightarrow\)\(M=\left(a-2005\right)^{2006}+\left(b-2005\right)^{2006}+\left(c-2005\right)^{2006}\)=\(\left(-2005\right)^{2006}+\left(-2005\right)^{2006}+\left(-2005\right)^{2006}\)=\(3.2005^{2006}\)

\(\left(x-\sqrt{11}\right)^2=0\)
\(\left(x-\sqrt{11}\right)=0\)
\(x=\sqrt{11}\)
\(\left(x-\sqrt{11}^2=0\right)\)
\(\left(x-\sqrt{11}\right)=0\)
\(x=\sqrt{11}\)

Đặt \(a=\sqrt{2006}-\sqrt{2005}\) , \(b=\sqrt{2006}+\sqrt{2005}\)
Ta sẽ chứng minh \(a=\frac{1}{b}\)
Ta có : \(a=\sqrt{2006}-\sqrt{2005}=\frac{\left(\sqrt{2006}-\sqrt{2005}\right).\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\frac{2006-2005}{\sqrt{2006}+\sqrt{2005}}\)
\(=\frac{1}{\sqrt{2006}+\sqrt{2005}}=\frac{1}{b}\)
Vậy a và b là hai số nghịch đảo.
Đầu tiên nhắc lại định nghĩ hai số nghịch đảo: Hai số được gọi là nghịch đảo nếu tích của chúng bằng 1.
Vd: $ab=1\implies $ a và b là hai số nghịch đảo của nhau và ngược lại nếu a và b là hai số nghịch đảo của nhau thì $ab=1$.
Áp dụng vào bài toán trên ta có: $(\sqrt{2006}-\sqrt{2005})(\sqrt{2006}-\sqrt{2005})=1\implies $ hai số trên là nghịch đảo của nhau.