Tìm đạo hàm của mỗi hàm số sau trên R.
LG a
y=ax2 (a là hằng số)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
TM
Tìm đạo hàm của hàm số \(y=\dfrac{a^3}{\sqrt{a^2-x^2}}\) (a là hằng số)
Giúp mình với ạ, mình cảm ơnn
1
HT
26 tháng 4 2021
\(y'=\dfrac{\left(a^3\right)'.\sqrt{a^2-x^2}-\left(\sqrt{a^2-x^2}\right)'.a^3}{a^2-x^2}=\dfrac{-\dfrac{1}{2\sqrt{a^2-x^2}}\left(a^2-x^2\right)'.a^3}{a^2-x^2}\)
\(y'=\dfrac{x.a^3}{\sqrt{a^2-x^2}\left(a^2-x^2\right)}\)
CM
30 tháng 5 2018
a) Hàm hằng ⇒ Δy = 0
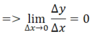
b) theo định lí 1
y = x hay y = x1 ⇒ y’= (x1)’= 1. x1-1 = 1. xo = 1.1 =1
CM
23 tháng 9 2017
Đáp án A.
Mệnh đề 3 sai ví dụ hàm số y=|x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó.
Mệnh đề 4 đúng vì nếu hàm số y=f(x) có đạo hàm trên [a;b] thì hàm số liên tục trên [a;b] do đó hàm số có nguyên hàm trên [a;b]
17 tháng 2 2022
a, y = ax^2 đi qua B(2;4)
<=> 4a = 4 <=> a = 1
b, bạn tự vẽ
17 tháng 2 2022
a: Thay x=2 và y=4 vào hàm số, ta được:
\(a\cdot4=4\)
hay a=1
b: Thay x=2 và y=4 vào hàm số, ta được:
4a=4
hay a=1
Đặt \(y=f\left(x\right)=ax^2\)
Chọn \(x=x_0\inℝ\) bất kỳ. Gọi \(\Delta x\) là số gia của biến \(x\)
Khi đó \(\Delta y=f\left(x_0+\Delta x\right)-f\left(x_0\right)\)
\(=a\left(x_0+\Delta x\right)^2-ax_0^2\)
\(=ax_0^2+2ax_0\Delta x+\left(\Delta x\right)^2-ax_0^2\)
\(=2ax_0\Delta x+\left(\Delta x\right)^2\)
Do đó \(\lim\limits_{\Delta x\rightarrow0}\dfrac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\rightarrow0}\dfrac{2ax_0\Delta x+\left(\Delta x\right)^2}{\Delta x}=\lim\limits_{\Delta x\rightarrow0}\left(2ax_0+\Delta x\right)\) \(=2ax_0\)
Như vậy, \(\left(ax^2\right)'=2ax\) với a là hằng số.
Kudo Shinichi = Conan !?