Phân thức \dfrac{7x+4}{(10x - 13 + 4x) -(4 - x)}(10x−13+4x)−(4−x)7x+4 xác định khi x...
Đọc tiếp
Phân thức \dfrac{7x+4}{(10x - 13 + 4x) -(4 - x)}(10x−13+4x)−(4−x)7x+4 xác định khi x \nex=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
5 tháng 7 2017
Mấy bài kia phá tung tóe rồi rút gọn hết sức xong thay x vào, làm câu c thôi nhé:
c) \(C=x^{14}-10x^{13}+10x^{12}-10x^{11}+...+10x^2-10x+10\)
riêng câu này ta thay x = 9 vào luôn, vậy ta có:
\(C=9^{14}-10\cdot9^{13}+10\cdot9^{12}-10\cdot9^{11}+...+10\cdot9^2-10\cdot9+10\)
\(=9^{14}-\left(9+1\right)\cdot9^{13}+\left(9+1\right)\cdot9^{12}-\left(9+1\right)\cdot9^{11}+...+\left(9+1\right)\cdot9^2-\left(9+1\right)\cdot9+10\)
\(=9^{14}-9^{14}-9^{13}+9^{13}+9^{12}-9^{12}-9^{11}+...+9^3+9^2-9^2-9+10\)
\(=-9+10\)
\(=1\)
NN
29 tháng 11 2017
a) \(\dfrac{4x-1}{3x^2y}-\dfrac{7x-1}{3x^2y}\)
\(=\dfrac{\left(4x-1\right)-\left(7x-1\right)}{3x^2y}\)
\(=\dfrac{4x-1-7x+1}{3x^2y}\)
\(=\dfrac{-3x}{3x^2y}\)
\(=\dfrac{-1}{xy}\)
b) \(\dfrac{4x+5}{2x-1}-\dfrac{5-9x}{2x-1}\)
\(=\dfrac{\left(4x+5\right)-\left(5-9x\right)}{2x-1}\)
\(=\dfrac{4x+5-5+9x}{2x-1}\)
\(=\dfrac{13x}{2x-1}\)
c) \(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)
\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)
\(=\dfrac{11x+\left(x-18\right)}{2x-3}\)
\(=\dfrac{11x+x-18}{2x-3}\)
\(=\dfrac{12x-18}{2x-3}\)
\(=\dfrac{6\left(2x-3\right)}{2x-3}\)
\(=\dfrac{6}{1}\)
\(=6\)
d) \(\dfrac{2x-7}{10x-4}-\dfrac{3x+5}{4-10x}\)
\(=\dfrac{2x-7}{10x-4}+\dfrac{3x+5}{10x-4}\)
\(=\dfrac{\left(2x-7\right)+\left(3x+5\right)}{10x-4}\)
\(=\dfrac{2x-7+3x+5}{10x-4}\)
\(=\dfrac{5x-2}{10x-4}\)
\(=\dfrac{5x-2}{2\left(5x-2\right)}\)
\(=\dfrac{1}{2}\)
HB
1
20 tháng 10 2018
Đặt \(\hept{\begin{cases}x^2+3x-4=a\\3x^2+7x+4=b\end{cases}\Rightarrow4x^2+10x=a+b}\)
\(\left(x^2+3x-4\right)^3+\left(3x^2+7x+4\right)^3=\left(4x^2+10x\right)^3\)
\(\Rightarrow a^3+b^3=\left(a+b\right)^3\)
\(\Rightarrow a^3+b^3=a^3+b^3+3ab\left(a+b\right)\)
\(\Rightarrow3ab\left(a+b\right)=0\)
Nếu \(a=0\Rightarrow x^2+3x-4=0\Rightarrow x\left(x+4\right)-\left(x+4\right)=0\Rightarrow\left(x+4\right)\left(x-1\right)=0\Rightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)
Nếu \(b=0\Rightarrow3x^2+7x+4=0\Rightarrow3x\left(x+1\right)+4\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(3x+4\right)=0\Rightarrow\orbr{\begin{cases}x=-1\\x=-\frac{4}{3}\end{cases}}\)
Nếu \(a+b=0\Rightarrow4x^2+10x=0\Rightarrow2x\left(2x+5\right)=0\Rightarrow\orbr{\begin{cases}x=0\\x=-\frac{5}{2}\end{cases}}\)
HN
1 tháng 7 2021
a)
⇔ \(x^2-16=9\)
⇔ \(x^2=25\)
⇔ \(x=\pm5\)
b)
⇔ \(x^2-4x+4-25x^2+20x-4=0\)
⇔ \(16x-24x^2=0\)
⇔ \(8x\left(2-3x\right)=0\)
⇒ \(\left[{}\begin{matrix}x=0\\2-3x=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy \(x=0\) hoặc \(x=\dfrac{2}{3}\)
c)
⇔ \(3x^2-10x-20=0\)
⇔ \(x^2-2.x.\dfrac{5}{3}+\dfrac{25}{9}-\dfrac{205}{9}=0\)
⇔ \(\left(x-\dfrac{5}{3}\right)^2=\dfrac{205}{9}\)
⇒ \(\left[{}\begin{matrix}x-\dfrac{5}{3}=\sqrt{\dfrac{205}{9}}\\x-\dfrac{5}{3}=-\sqrt{\dfrac{205}{9}}\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{\sqrt{\text{205}}}{\text{3}}+\dfrac{5}{3}\\x=-\dfrac{\sqrt{\text{205}}}{\text{3}}+\dfrac{5}{3}\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{15+\text{9}\sqrt{\text{205}}}{\text{9}}\\\text{x}=-\dfrac{15+\text{9}\sqrt{\text{205}}}{\text{9}}\end{matrix}\right.\)
Vậy...
d)
⇔ \(\left(x^2+x\right)^2-49=\left(x^2+x\right)^2-7x\)
⇔ 7x = 49
⇔ x=7
Vậy...
1 tháng 3 2022
a: \(\Leftrightarrow x^2\left(9x^2-4\right)=0\)
\(\Leftrightarrow x^2\left(3x-2\right)\left(3x+2\right)=0\)
hay \(x\in\left\{0;\dfrac{2}{3};-\dfrac{2}{3}\right\}\)
b: \(\Leftrightarrow2x^4-4x^2+3x^2-6=0\)
\(\Leftrightarrow x^2-2=0\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
d: \(\Leftrightarrow x^4-9x^2+6x^2-54=0\)
\(\Leftrightarrow x^2-9=0\)
=>x=3 hoặc x=-3
2 tháng 6 2022
Câu 1:
\(\dfrac{x^2-10x+21}{x^3-7x^2+x-7}=\dfrac{\left(x-7\right)\left(x-3\right)}{\left(x-7\right)\left(x^2+1\right)}=\dfrac{x-3}{x^2+1}\)
\(\dfrac{2x^2-x-15}{2x^3+5x^2+2x+5}=\dfrac{2x^2-6x+5x-15}{\left(2x+5\right)\left(x^2+1\right)}=\dfrac{\left(2x+5\right)\left(x-3\right)}{\left(2x+5\right)\left(x^2+1\right)}=\dfrac{x-3}{x^2+1}\)
Do đó: \(\dfrac{x^2-10x+21}{x^3-7x^2+x-7}=\dfrac{2x^2-x-15}{2x^3+5x^2+2x+5}\)
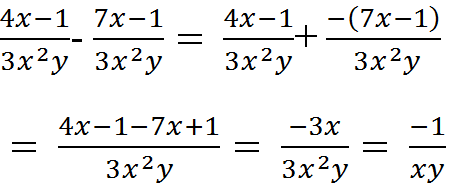
Phân thức \(\frac{7x+4}{\left(10x-13+4x\right)-\left(4-x\right)}\)khi :
\(10x-13+4x-\left(4-x\right)\ne0\)
\(\Leftrightarrow10x-13+4x-4+x\ne0\)
\(\Leftrightarrow15x-17\ne0\)
\(\Leftrightarrow x\ne\frac{17}{15}\)
Phân thức \(\frac{7x+4}{\left(10x-13+4x\right)-\left(4-x\right)}\)xác đinhk khi
\(\left(10x-13+4x\right)-\left(4-x\right)\ne0\)
\(\Leftrightarrow10x-13+4x-4+x\ne0\)
\(\Leftrightarrow15x-17\ne0\)
\(\Leftrightarrow15x\ne17\)
\(\Leftrightarrow x\ne\frac{17}{15}\)
Vậy phân thức \(\frac{7x+4}{\left(10x-13+4x\right)-\left(4-x\right)}\)được xác đinh khi \(x\ne\frac{17}{15}\)