\(1.31:\) Cho đường thẳng \(d\) và hai điểm \(A,B\) cùng thuộc một nửa mặt phẳng bờ \(d\). Hai điểm \(E,F\) thay đổi trên \(d\) sao cho \(\overrightarrow{EF}\) không đổi. Xác định vị trí của hai điểm \(E,F\) để \(AE+BF\) nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)

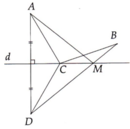
Lấy D là điểm đối xứng, với A qua d. Theo tính chất đường trung trực: CA = CD.
Do đó CA + CB = CD + CB.
Gọi M là giao điểm của BD và d.
Nếu C không trùng với M thì xét tam giác BCD, ta có: CB + CD > BD hay CA + CB > BD (1).
Nếu C trùng với M thì:
CA + CB = MA + MB = MD + MB = BD (2).
So sánh (1) và (2) ta thấy điểm C trùng M hay C là giao điểm của BD và d thì giá trị của tổng CA + CB là nhỏ nhất.
Chú ý: Điểm C tìm được ở vị trí M như vậy là điểm duy nhất. Thật vậy, nếu lấy E đối xứng với B qua d thì AE vẫn cắt d ở M đúng vị trí mà BD cắt d.

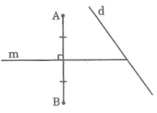
* Nếu AB không vuông góc với d
- Vì điểm C cách đều hai điểm A và B nên C nằm trên đường trung trực của AB.
- Điểm C ∈ d
Vậy C là giao điểm của đường trung trực của AB và đường thẳng d.
Cần dựng đường thẳng m là đường trung trực của đoạn thẳng AB cắt đường thẳng d tại C.
Vậy C là điểm cần tìm.
* Nếu AB vuông góc với d
Khi đó đường trung trực của AB song song với đường thẳng d nên không tồn tại điểm C.
GỮZLNIBCEVY6XW4ZNIMP
Chứng minh rằng:
\(a;\) \(2n+11...1\) ( \(n\) chữ số) chia hết \(3\)
\(b;10^n+18n-1⋮27\)
\(c;10^n+72n-1⋮81\)