cho hình thoi ABCD có góc A bằng 90* tính số đo các góc còn lại của hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
1
19 tháng 11 2017
tihs chất hình thoi là 2 goc đối bằng nhau
Do C là góc đối của A mà A = 40 độ nên C = 40 độ
2 goc B và D cũng dối nhau nên bằng nhau
góc B cộng D = 360 - 40 - 40 = 280độ
=> B=D = 280:2=140 độ
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 12 2023
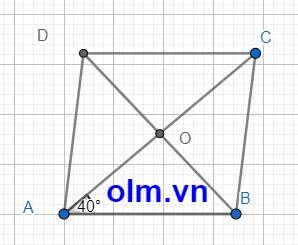
Vì ABCD là hình thoi nên ⇒ tam giác ABD cân tại A
Vì O là trung điểm DB nên AO là truyến là đường phân giác của tam giác ABD
⇒ \(\widehat{DAO}\) = 400
⇒ \(\widehat{DAB}\) = 400 + 400 = 1800
⇒ \(\widehat{ADC}\) = 1800 - 800 = 1000
⇒ \(\widehat{DCB}\) = 1800 - 1000 = 800
\(\Rightarrow\) \(\widehat{ABC}\) = 1800 - 800 = 1000
7 tháng 8 2023
1) \(S_{ABCD}=\dfrac{1}{2}.AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.50\sqrt[]{3}}{10}=10\sqrt[]{3}\left(cm\right)\)
Gọi O là giao điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}OA=\dfrac{1}{2}AC=5\left(cm\right)\\OB=\dfrac{1}{2}BD=5\sqrt[]{3}\left(cm\right)\end{matrix}\right.\)
Xét Δ vuông OAB có :
\(AB^2=OA^2+OC^2=25+25.3=100\left(cm^2\right)\left(Pitago\right)\)
\(\Rightarrow AB=10\left(cm\right)\)
2) Xét Δ vuông OAB có :
\(AB=2OA=10\left(cm\right)\)
⇒ Δ OAB là Δ nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABD}=30^o\\\widehat{BAC}=60^o\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2\widehat{BAC}\\\widehat{ADC}=\widehat{ABC}=2\widehat{ABD}\end{matrix}\right.\) (tính chất hình thoi)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2.60=120^o\\\widehat{ADC}=\widehat{ABC}=2.30=60^o\end{matrix}\right.\)
LA
2 tháng 12 2016
-Gọi AC cắt BD tại O. Ta có MN=OB=OD(=1/2.BD).
-Ta có: tam giác BMD vuông tại M có O là trung điểm của BD nên MO=1/2.BD.
tam giác BND vuông tại N có O là trung điểm của BD nên NO=1/2.BD.
Suy ra: MO=ON=MN=BO=OD. => tam giác MON đều => góc MON=60 độ.
-Mà góc MOD=góc NOD=1/2. góc MON=30 độ và OM=OD => góc MDO=75 độ. => góc ADC=góc ABC=2.góc MDO= 150 độ.
=> góc BAD=góc BCD= 30 độ.
Vậy góc A và góc C của hình thoi ABCD bằng 30 độ; góc B và góc D của hình thoi bằng 150 độ.