b=1.2+2.3+3.4+...+2023.2024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
=5(1-1/2+1/2-1/3+...+1/2023-1/2024)
=5*2023/2024
=10115/2024
P
Phong
CTVHS
1 tháng 11 2023
a) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)
\(2A=2\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\right)\)
\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{101}}\)
\(2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{100}}\)
\(A=1-\dfrac{1}{2^{100}}\)
b) \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2023\cdot2024}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\)
\(=1-\dfrac{1}{2024}\)
\(=\dfrac{2024}{2024}-\dfrac{1}{2024}\)
\(=\dfrac{2023}{2024}\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2024
\(\dfrac{C_n^k}{\left(k+1\right)\left(k+2\right)}=\dfrac{n!}{\left(k+1\right)\left(k+2\right).k!\left(n-k\right)!}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}.\dfrac{\left(n+2\right)!}{\left(n+2-\left(k+2\right)\right)!\left(k+2\right)!}\)
\(=\dfrac{1}{\left(n+1\right)\left(n+2\right)}.C_{n+2}^{k+2}\)
Đặt tổng trên là A
\(\Rightarrow A=\dfrac{-1.C_{2024}^3}{2023.2024}+\dfrac{2.C_{2024}^4}{2023.2024}+\dfrac{-3.C_{2024}^5}{2023.2024}+...+\dfrac{2022.C_{2024}^{2024}}{2023.2024}\)
\(=\dfrac{1}{2023.2024}\left(-1.C_{2024}^3+2.C_{2024}^4+...+2022.C_{2024}^{2024}\right)=\dfrac{1}{2023.2024}.B\)
Xét \(C=-2.\left(-C_{2024}^3+C_{2024}^4-C_{2024}^5+...+C_{2024}^{2024}\right)\)
\(\Rightarrow B-C=-3C_{2024}^3+4C_{2024}^4-5C_{2024}^5+...+2024.C_{2024}^{2024}\)
Ta có:
\(k.C_n^k=\dfrac{n!.k}{\left(n-k\right)!.k!}=n.\dfrac{\left(n-1\right)!}{\left(\left(n-1\right)-\left(k-1\right)\right)!.\left(k-1\right)!}=n.C_{n-1}^{k-1}\)
\(\Rightarrow B-C=-2024.C_{2023}^2+2024C_{2023}^3+...+2024.C_{2023}^{2023}\)
\(=-2024\left(C_{2023}^2-C_{2023}^3+...-C_{2023}^{2023}\right)\)
Xét khai triển:
\(\left(1-x\right)^k=C_k^0-xC_k^1+x^2C_k^2+...+\left(-1\right)^kx^k.C_k^k\)
Thay \(k=2024\); \(x=1\)
\(\Rightarrow0=C_{2024}^0-C_{2024}^1+C_{2024}^2-C_{2024}^3+...+C_{2024}^{2024}\)
\(\Rightarrow-C_{2024}^3+...+C_{2024}^{2024}=C_{2024}^1-C_{2024}^2-1\)
\(\Rightarrow C=-2\left(C_{2024}^1-C_{2024}^2-1\right)=-2\left(2023-C_{2024}^2\right)\)
Thay \(k=2023;x=1\)
\(\Rightarrow0=C_{2023}^0-C_{2023}^1+C_{2023}^2+...-C_{2023}^{2023}\)
\(\Rightarrow C_{2023}^2-C_{2023}^3+...-C_{2023}^{2023}=C_{2023}^1-1=2022\)
\(\Rightarrow B-C=-2024.2022\)
\(\Rightarrow B=C-2022.2024=-2\left(2023-C_{2024}^2\right)-2022.2024\)
\(=-2.2023+2023.2024-2022.2024\)
\(=-2022\)
\(\Rightarrow A=\dfrac{-2022}{2023.2024}\)
TT
1
25 tháng 8 2017
Ta có : S = 1.2 + 2.3 + 3.4 + ..... + 32.33
=> 3S = 1.2.3 - 1.2.3 + 2.3.4 - 2.3.4 + ...... + 32.33.34
=> 3S = 32.33.34
=> S = \(\frac{32.33.34}{3}=11968\)
KG
Cho A=1/1.2 + 1/2.3 + + 1/ 3.4+...+1/49.50 ; B = 1.2+2.3+3.4+4.5+5.6+...+49.50
Tính 50 mủ 2 A – B/17
0
PM
2
VD
23 tháng 1 2022
3C=1.2.3+2.3.(4-1)+3.4.(5-2)+...+2014.2015.(2016-2013)
3C=2014.2015.2016
C=2014.2015.2016:3
DD
Đoàn Đức Hà
Giáo viên
12 tháng 7 2021
\(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{49.50}\)
\(=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{50-49}{49.50}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{49}-\frac{1}{50}\)
\(=1-\frac{1}{50}=\frac{49}{50}\)
\(B=1.2+2.3+3.4+...+49.50\)
\(3B=1.2.3+2.3.3+3.4.3+...+49.50.3\)
\(=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+49.50.\left(51-48\right)\)
\(=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+49.50.51-48.49.50\)
\(=49.50.51\)
\(B=\frac{49.50.51}{3}=49.50.17\)
\(50^2.A-\frac{B}{17}=49.50-49.50=0\)
PT
1
PT
1
NT
1
20 tháng 4 2016
C=1*2+2*3+3*4+...+98*99
C=2+6+12+...+9702
C=2+9702
C=9704
vay C=9704
D=(1*99+2*99+3*99+...+99*99)-(1*2+2*3+3*4+...+98*99)
D=(99+198+297+...+9801)-(2+6+12+...+9702)
D=(99+9801)-(2+9702)
D=9900-9704
D=196
vay D=196
ai di qua dong tinh thi nho h cho minh nhe
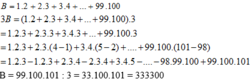
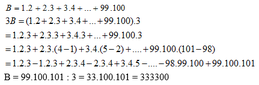
\(b=1\cdot2+2\cdot3+3\cdot4+...+2023\cdot2024\\ 3b=1\cdot2\cdot3+2\cdot3\cdot3+3\cdot3\cdot4+...+2023\cdot2024\cdot3\\ 3b=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+...+2023\cdot2024\cdot\left(2025-2022\right)\\ 3b=1\cdot2\cdot3+2\cdot3\cdot4-1\cdot2\cdot3+...+2023\cdot2024\cdot2025-2022\cdot2023\cdot2024\\ 3b=\left(1\cdot2\cdot3-1\cdot2\cdot3\right)+\left(2\cdot3\cdot4-2\cdot3\cdot4\right)+...+\left(2022\cdot2023\cdot2024-2022\cdot2023\cdot2024\right)+2023\cdot2024\cdot2025\\ 3b=8291467800\\ b=2763822600\)
B = 1.2 + 2.3 + ... + 2023.2024
B = \(\dfrac{1}{3}\).(1.2.3 + 2.3.3 + ... + 2023.2024.3)
B = \(\dfrac{1}{3}\).[1.2.3 + 2.3.(4-1) + ...+ 2023.2024.(2025-2022)]
B = \(\dfrac{1}{3}\).[1.2.3 + 2.3.4- 1.2.3 + ... + 2023.2024.2025 - 2022.2023.2024]
B = \(\dfrac{1}{3}\).2023.2024.2025
B = 2023.2024.(2025.\(\dfrac{1}{3}\))
B = 4094552.675
B = 2763822600