A=\frac{2}{1\cdot \:9}+\frac{2}{3\cdot \:15}+\frac{2}{5\cdot \:21}+\frac{2}{9\cdot \:33}+\frac{2}{11\cdot \:39}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
26 tháng 6 2021
Tham khảo:
a) Tìm giá trị phân số của một số cho trước :
Muốn tìm m/n của một số b cho trước, ta nhân m/n với b. (Với m,n ∈ N,n ≠ 0)
Vd : tính 1/3 của 9
1/3 của 9 là : 1/3 × 9 = 3
b) Quy tắc tìm một số biết giá trị một phân số của nó:
Muốn tìm một số biết m/n của nó bằng a thì số đó được tính bằng a: (m/n) (m,n ∈ N∗)
Ví dụ: Tìm một số biết 3/4 của nó bằng 15
Số cần tìm là: 15 : 3/4 = 20
c)
- Tỉ số của hai số:
Thương trong phép chia số a cho số b (b ≠ 0) gọi là tỉ số của a và b
Kí hiệu a:b hoặc a/b
Ví dụ: Tỉ số của 5 và 7 là 5 : 7 = 5/7
- Tỉ số phần trăm:
Muốn tìm tỉ số phần tram của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào kết quả: a.100/b %
Ví dụ: Tỉ số phần trăm của 1 kg và 2 kg là:
1 : 2 × 100 = 50%
28 tháng 6 2021
a, Tìm giá trị phân số của một số cho trước
- Quy tắc: Muốn tìm \(\dfrac{m}{n}\) của b cho trước, ta tính \(b.\dfrac{m}{n}\)
VD: 0,25 của 1 giờ
Đổi 1 giờ= 60 phút
60.0,25=15 phút
b, Tìm một số biết giá trị phân số của nó:
- Quy tắc: Muốn tìm một số biết \(\dfrac{m}{n}\) của số đó, ta lấy \(a:\dfrac{m}{n}\)
VD: \(\dfrac{2}{3}\) của nó bằng 7,2: 23=10,823=10,8
c, Tìm tỉ số của a và b
- Quy tắc: Thương trong phép chia a cho b (b≠0) là tỉ số của a và b
VD: Tỉ số giữa a và b là a:b hoặc \(\dfrac{a}{b}\)
26 tháng 4 2021
a, Tìm giá trị phân số của một số cho trước
- Quy tắc: Muốn tìm \(\dfrac{m}{n}\) của b cho trước, ta tính b.\(\dfrac{m}{n}\)
VD: 0,25 của 1 giờ
Đổi 1 giờ= 60 phút
60.0,25=15 phút
b, Tìm một số biết giá trị phân số của nó:
- Quy tắc: Muốn tìm một số biết \(\dfrac{m}{n}\) của số đó, ta lấy a:\(\dfrac{m}{n}\)
VD: \(\dfrac{2}{3}\) của nó bằng 7,2: \(\dfrac{2}{3}=10,8\)
c, Tìm tỉ số của a và b
- Quy tắc: Thương trong phép chia a cho b (b≠0) là tỉ số của a và b
VD: Tỉ số giữa a và b là a:b hoặc \(\dfrac{a}{b}\)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a)
\(\begin{array}{l}M = \frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\\ = \frac{{ - 5}}{{56}} + \frac{{ - 11}}{{56}} = \frac{{ - 16}}{{56}} = \frac{{ - 2}}{7}\end{array}\)
b)
\(\begin{array}{l}M = \frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\\ = \frac{1}{7}.[(\frac{{ - 5}}{8}) + (\frac{{ - 11}}{8})]\\ = \frac{1}{7}.\frac{{ - 16}}{8}\\ = \frac{1}{7}.( - 2)\\ = \frac{{ - 2}}{7}\end{array}\)
CM
5 tháng 11 2018
Cách 1:Không áp dụng tính phân phối:
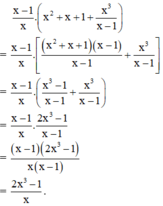
Cách 2: Áp dụng tính chất phân phối: A( B+ C)= AB + AC
14 tháng 2 2023
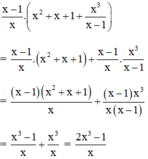
a) c1 := -2/-5+-5/-6+4/5
=2/5+5/6+4/5
=12/30+25/30+24/30
=61/30
c2:=(2/5+4/5)+4/5
=(2/5+4/5)+5/6
=6/5+5/6
=36/30+25/30
=61/30
b)c1:=-3/-4+11/-15+-1/2
=3/4+-11/15+-1/2
=45/60+-44/30+-30/60
-29/30
c2:=3/4+(-11/15+-1/2)
=(3/4+-1/2)+-11/15
=(3/4+-2/4)+-11/5
=1/4+-11/15
=15/60+-44/60
=-29/60
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
a) Cách 1:
\(\begin{array}{l}\left( {\frac{{ - 2}}{{ - 5}} + \frac{{ - 5}}{{ - 6}}} \right) + \frac{4}{5} = \frac{2}{5} + \frac{5}{6} + \frac{4}{5}\\ = \frac{{12}}{{30}} + \frac{{25}}{{30}} + \frac{{24}}{{30}} = \frac{{61}}{{30}}\end{array}\)
Cách 2:
\(\begin{array}{l}\left( {\frac{{ - 2}}{{ - 5}} + \frac{{ - 5}}{{ - 6}}} \right) + \frac{4}{5} = \left( {\frac{2}{5} + \frac{4}{5}} \right) + \frac{5}{6}\\ = \frac{6}{5} + \frac{5}{6} = \frac{{36}}{{30}} + \frac{{25}}{{30}} = \frac{{61}}{{30}}\end{array}\)
b) Cách 1:
\(\begin{array}{l}\frac{{ - 3}}{{ - 4}} + \left( {\frac{{11}}{{ - 15}} + \frac{{ - 1}}{2}} \right) = \frac{3}{4} + \frac{{ - 11}}{{15}} + \frac{{ - 1}}{2}\\ = \frac{{45}}{{60}} + \frac{{ - 44}}{{60}} + \frac{{ - 30}}{{60}}\\ = \frac{{ - 29}}{{60}}\end{array}\).
Cách 2:
\(\begin{array}{l}\frac{{ - 3}}{{ - 4}} + \left( {\frac{{11}}{{ - 15}} + \frac{{ - 1}}{2}} \right) = \frac{3}{4} + \frac{{ - 11}}{{15}} + \frac{{ - 1}}{2}\\ = \left( {\frac{3}{4} + \frac{{ - 1}}{2}} \right) + \frac{{ - 11}}{{15}}\\ = \left( {\frac{3}{4} + \frac{{ - 2}}{4}} \right) + \frac{{ - 11}}{{15}}\\ = \frac{1}{4} + \frac{{ - 11}}{{15}}\\ = \frac{{15}}{{60}} + \frac{{ - 44}}{{60}}\\ = \frac{{ - 29}}{{60}}\end{array}\)
29 tháng 8 2020
A = 101 x 50
B = 50 x 49 + 53 x 50 = 50 x (49+53) = 50 x 102
Có 101<102 => 50 x 101 < 50 x 102
=> A<B
ẢO THẬT ĐẤY! <:0