tìm x thuộc z biết
a, -5x - 100 = -5
b, 2.(30-x)+(-82) =-12
c, 16 - 5x = 9-100
d,(2x +4).(3x-9)= 0
giúp mik nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

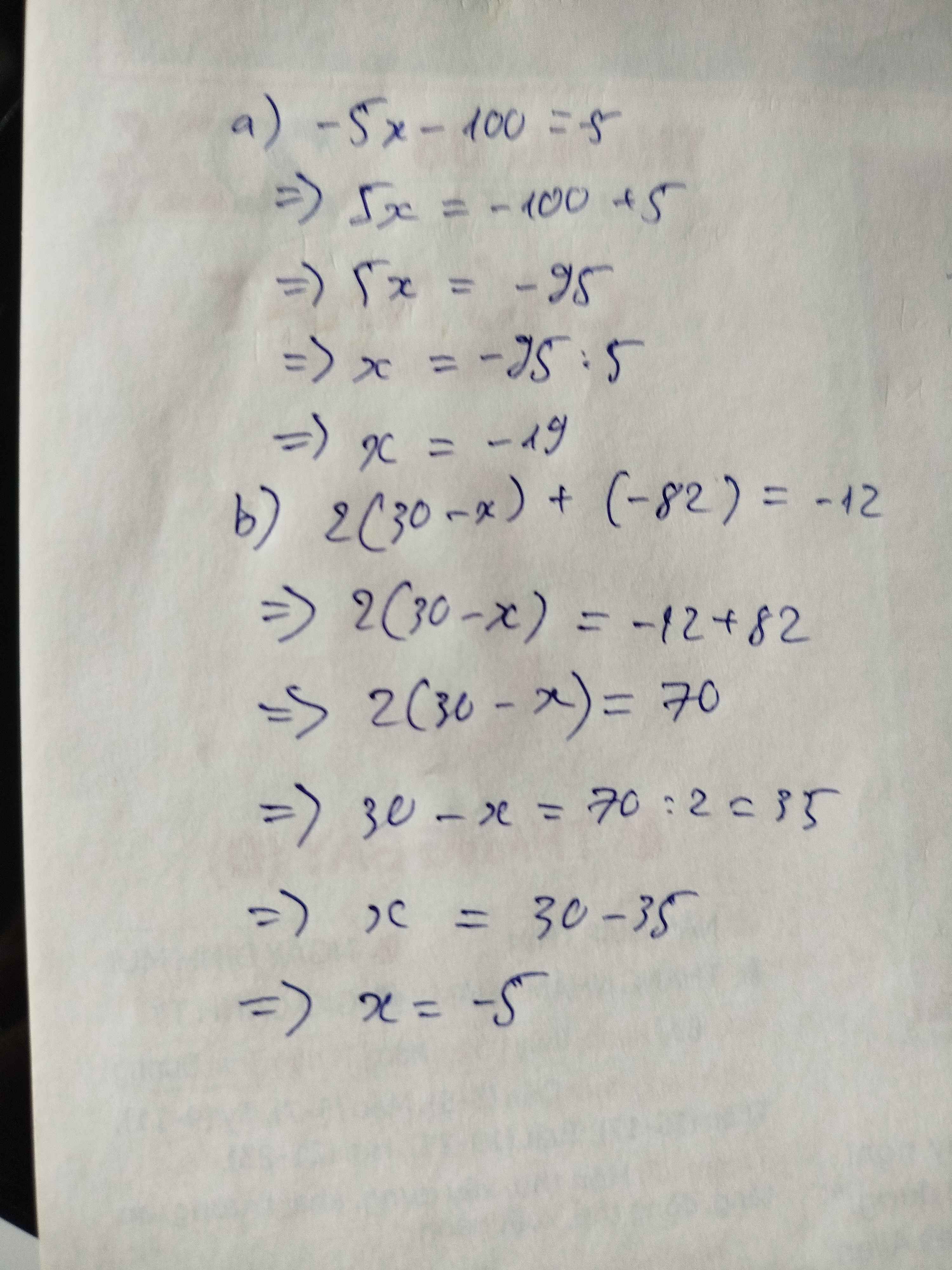


Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1

a) \(5x + 3y < 20\)
Đây là bất phương trình bậc nhất hai ẩn.
Chọn \(x = 0;y = 0\)
Khi đó bất phương trình tương đương với 5.0+3.0
Vậy (0;0) là một nghiệm của bất phương trình trên.
b) \(3x - \frac{5}{y} > 2\)
Đây không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.

a: Phương trình có dạng ax+b=0 khi a<>0 được gọi là phương trình bậc nhất một ẩn
Phương trình 2x-5=2x+3 là phương trình bậc nhất một ẩn
c: Hai phương trình tương đương là hai phương trình có cùng tập nghiệm

a) PT bậc nhất một ẩn là: x-2=0; 4-0,2x=0
b) Giải:
x-2=0 (*)
⟺ x=-2
Vậy tập nghiệm của pt (*) là S={-2}
4-0,2x=0 (**)
⟺-0,2x=-4
⟺x=-4/-0,2=20
Vậy tập nghiệm của pt (**) là S={20}

a, Thay \(m=1\) vào \(\left(1\right)\)
\(\Rightarrow x^2-7x+1=0\\ \Delta=\left(-7\right)^2-4.1.1=45\\ \Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{7+3\sqrt{5}}{2}\\x_2=\dfrac{7-3\sqrt{5}}{2}\end{matrix}\right.\)
b, \(\Delta=\left(-7\right)^2-4.m=49-4m\)
phương trình cs nghiệm \(49-4m\ge0\\ \Rightarrow m\le\dfrac{49}{4}\)
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x_1+x_2=7\\x_1x_2=m\end{matrix}\right.\)
\(x^2_1+x^2_2=29\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\\ \Leftrightarrow7^2-2.m-29=0\\ \Leftrightarrow20-2m=0\\ \Rightarrow m=10\left(t/m\right)\)
Vậy \(m=10\)

\(\Delta'=\left(m+1\right)^2-2m-10=m^2-9\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)
a.
\(P=x_1^2+x_2^2+6x_1x_2=\left(x_1+x_2\right)^2+4x_1x_2\)
\(P=4\left(m+1\right)^2+4\left(2m+10\right)\)
\(P=4m^2+16m+44=\left(4m^2+16m+12\right)+32\)
\(P=4\left(m+1\right)\left(m+3\right)+32\ge32\)
\(P_{min}=32\) khi \(m=-3\)
b.
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=2m+10\end{matrix}\right.\)
Trừ vế cho vế:
\(x_1+x_2-x_1x_2=-8\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m