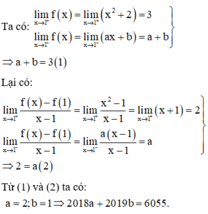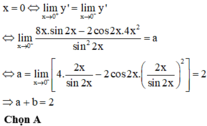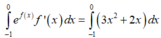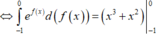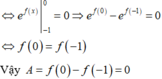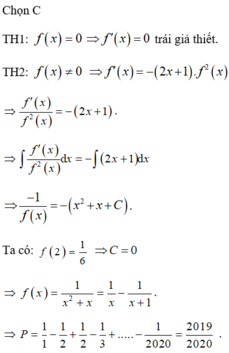Tính giá trị của biểu thức A= x'' -8x'* +8x" - 8x' +. .- 8x7 +8x- 5 tại x =7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do f có đạo hàm tại điểm ![]() nên f liên tục tại điểm
nên f liên tục tại điểm ![]() .
.
Khi đó
![]()
a + b + 2 = 2a + b + 1 nên a = 1
Với a = 1, hàm số f(x) trở thành
f x = x + 2 a + b ; x < 1 a x 2 + b x + 2 ; x ≥ 1
f(x) có đạo hàm tại điểm x 0 = 1 khi và chỉ khi
lim x → 1 + f x - f 1 x - 1 = lim x → 1 f x - f 1 x - 1 ⇔ lim x → 1 + x 2 + b x + 2 - b - 3 x - 1 = lim x → 1 x + 2 + b - b - 3 x - 1 ⇔ lim x → 1 + x + b + 1 = l i m 1 ⇔ b + 2 = 1 ⇒ - 1
Suy ra a + b = 0. Vậy P = 5.
Đáp án cần chọn là D

a) Thay x = -1 và y = 3 vào A, ta được :
A = 2.(-1)[(-1) + 3] - (-1) + 7 - 3
A = -2.2 + 1 + 4
A = -4 + 5
A = 1
b) |y| = 3 => \(\orbr{\begin{cases}y=3\\y=-3\end{cases}}\)
*Thay x =-1 và y = 3 vào biểu thức :
Phần này bạn sẽ làm ý như câu a vậy :33
*Thay x = -1 và y =-3 vào A, ta được :
A = 2.(-1).[(-1) + (-3)] - (-1) + 7 - (-3)
A = -2.(-4) + 1 + 7 + 3
A = 8 + 11
A = 19

\(\left(x+3\right)^2=x^2+6x+9\le x^2+\left(9x^2+1\right)+9=10\left(x^2+1\right)\)
Suy ra: \(P=\dfrac{x+3}{\sqrt{x^2+1}}\le\sqrt{10}\)
Vậy \(MaxP=\sqrt{10}\) (khi \(x=\dfrac{1}{3}\))

Chọn đáp án A
Từ giả thiết, ta có
![]()
![]()
![]()
![]()
Suy ra
![]()
Với x = π 3 ta có
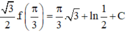
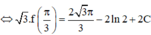
Với x = π 6 ta có
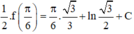
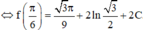
Suy ra
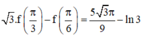
![]()
![]()