Giải bài toán bằng cách lập phương trình
bài 1: 1 ô tô đi trên quãng đường dài 400km.Khi đi được 180km thì ô tô tăng vận tốc thêm 10km/h và đi hết quãng đường còn lại. Tính vận tốc ban đầu của ô tô, biết thời gian đi hết quãng đường là 8h
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bài toán 1: Một ô tô đi được quãng đường 170km với vận tốc 42,5 km/giờ. Tính thời gian ô tô đi được quãng đường đó.
Bài giải:
Thời gian ô tô đi là:
170 : 42,5 = 4 (giờ)
Đáp số: 4 giờ.
Nhận xét: Để tính thời gian đi của ô tô ta lấy quãng đường đi được chia cho quãng đường ô tô đi được trong 1 giờ hay vận tốc của ô tô.
Muốn tính thời gian ta lấy quãng đường chia cho vận tốc.
Ta có: t = s : v
b) Bài toán 2: Một ca nô đi với vận tốc 36km/giờ trên quãng đường sông dài 42km. Tính thời gian đi của ca nô trên quãng đường đó.
Bài giải:
Thời gian đi của ca nô là:
42 : 36 = \(\frac{7}{6}\) (giờ)
\(\frac{7}{6}\) (giờ) = \(1\frac{1}{6}\) giờ = 1 giờ 10 phút.
Đáp số: 1 giờ 10 phút.

Gọi thời gian dự định đi hết quãng đường là x.
Độ dài quãng đường AB là: S = v.t = 40x
Nửa quãng đường là S/2 = 40x/2 = 20x.
Nửa quãng đường đầu đi vs vtốc dự định (40km/h)
=> Thời gian đi hết nửa quãng đường đầu là: t1 = S : v1 = 20x : 40 = 1/2x
Nửa quãng đường đầu đi vs vtốc tăng hơn dự định 10km/h (50km/h)
=> Thời gian đi hết nửa quãng đường sau là t2 = S : v2 = 20x : 50 = 2/5x
Tổng thời gian đi hết quãng đường là: t = t1 + t2 = 1/2x + 2/5x = 9/10x
Do thực tế đến B sớm hơn dự kiến 1h nên ta có: x - 9/10x = 1 => x = 10 (h)
=> Độ dài quãng đường AB là S = 40.10 = 400 (km).

Thời gian ô tô đi quãng đường A-B kể cả thời gian nghỉ là:
9 giờ 45 phút - 7 giờ 30 phút = 2 giờ 15 phút
Thời gian ô tô đi quãng đường A-B không kể thời gian nghỉ là:
2 giờ 15 phút - 15 phút = 2 ( giờ )
Vận tốc của ô tô là:
100 : 2 = 50 ( km/giờ )
Vận tốc xe máy là:
50 x 60% = 30 ( km/giờ )
Thời gian ô tô đi quãng đường A-B kể cả thời gian nghỉ là:
9 giờ 45 phút - 7 giờ 30 phút = 2 giờ 15 phút
Thời gian ô tô đi quãng đường A-B không kể thời gian nghỉ là:
2 giờ 15 phút - 15 phút = 2 ( giờ )
Vận tốc của ô tô là:
100 : 2 = 50 ( km/giờ )
Vận tốc xe máy là:
50 x 60% = 30 ( km/giờ )
Đáp số: 30 km/giờ
(tick dùm mik ạ)

gọi x là vận tốc của xe thứ nhất, y là vận tốc của xe thứ 2
sau 5h thì xe thứ nhất gặp xe thứ 2 và hai xe đi ngược nhau nên ta có phương trình (1) là:
5x + 5y = 400 (km)
ta lại có khi xe thứ nhất giảm 10km/h và xe thứ 2 tăng 10km/h thì 2 xe gặp nhau tại chính giữa quảng đường nghĩa là x -10 = y + 10
nên ta có phương trình (2) là:
x - y = 20
từ trên ta có hệ phương trình
\(\left\{{}\begin{matrix}5x+5y=400\\x-y=20\end{matrix}\right.\)
giải hệ phương trình ta có x = 50km/h và y = 30km/h
vậy vận tốc xe thứ nhất là 50km/h và vận tốc xe thứ hai là 30km/h

Gọi vận tốc ô tô dự định đi quãng đường AB là x (km/h).
Có phương trình: 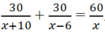
Giải ra được x = 30
Thời gian ô tô dự định đi là 2 giờ.

Gọi vận tốc của ô tô lúc đi từ A đến B là x(km/h)
(Điều kiện: x>0)
Vận tốc của ô tô lúc đi từ B về A là x+10(km/h)
Thời gian ô tô đi từ A đến B là \(\dfrac{400}{x}\left(giờ\right)\)
Thời gian ô tô đi từ B về A là \(\dfrac{400}{x+10}\left(giờ\right)\)
Theo đề, ta có phương trình:
\(\dfrac{400}{x}-\dfrac{400}{x+10}=2\)
=>\(\dfrac{400x+4000-400x}{x\left(x+10\right)}=2\)
=>2x(x+10)=4000
=>x(x+10)=2000
=>x^2+10x-2000=0
=>(x+20)(x-10)=0
=>\(\left[{}\begin{matrix}x+20=0\\x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-20\left(loại\right)\\x=10\left(nhận\right)\end{matrix}\right.\)
Vậy: vận tốc ô tô lúc đi từ A đến B là 10km/h

Gọi x (km/h)là vận tốc của ô tô đi từ A đến B.
\(\frac{400}{x}\)(h)là thời gian của ô tô đi từ A đến B
x + 10 (km/h) là vận tốc của ô tô đi từ B đến A
\(\frac{400}{x+10}\)(h) là thời gian của ô tô đi từ B đến A
Vì tổng thời gian đi và về là 18h, ta có pt:
\(\frac{400}{x}+\frac{400}{x+10}=18\)=) x = 40(km/h)
Vậy vận tốc của ô tô đi từ A đến B là 40 km/h
* Mk mới học lớp 8 nên giải bằng cách lập pt, có gì bn thông cảm.
Gọi vận tốc ban đầu của ô tô là x(km/h)
(Điều kiện: x>0)
Thời gian ô tô đi 180km đầu tiên là: \(\dfrac{180}{x}\left(giờ\right)\)
Độ dài quãng đường còn lại là 400-180=220(km)
Vận tốc của ô tô khi đi trên quãng đường còn lại là:
x+10(km/h)
Thời gian ô tô đi 220km còn lại là \(\dfrac{220}{x+10}\left(giờ\right)\)
Thời gian đi hết quãng đường là 8 giờ nên ta có:
\(\dfrac{180}{x}+\dfrac{220}{x+10}=8\)
=>\(\dfrac{45}{x}+\dfrac{55}{x+10}=2\)
=>\(\dfrac{45x+450+55x}{x\left(x+10\right)}=2\)
=>2x(x+10)=100x+450
=>x(x+10)=50x+225
=>\(x^2-40x-225=0\)
=>(x-45)(x+5)=0
=>\(\left[{}\begin{matrix}x=45\left(nhận\right)\\x=-5\left(loại\right)\end{matrix}\right.\)
Vậy: vận tốc ban đầu của ô tô là 45km/h
Giải:
Gọi vận tốc ban đầu của ô tô là: \(x\) (km/h) ; \(x\) > 0
Vận tốc lúc sau của ô tô là: \(x+10\) (km/h)
Thời gian ô tô đi lúc đầu là: 180 : \(x\) (giờ)
Thời gian ô tô đi lúc sau là: (400 - 180) : (\(x+10\)) = \(\dfrac{220}{x+10}\)
Theo bài ra ta có phương trình:
\(\dfrac{180}{x}\) + \(\dfrac{220}{x+10}\) = 8
\(\dfrac{45}{x}\) + \(\dfrac{55}{x+10}\) = 2
45(\(x+10\)) + 55\(x\) = 2.\(x\) (\(x+10\))
45\(x\) + 450 + 55\(x\) = 2\(x^2\) + 20\(x\)
2\(x^2\) + 20\(x\) - 55\(x\) - 45\(x\) = 450
2\(x^2\) + (20\(x\) - 55\(x\) - 45\(x\)) = 450
2\(x^2\) + (- 35\(x\) - 45\(x\)) = 450
2\(x^2\) - 80\(x\) = 450
\(x^2\) - 40\(x\) = 225
\(x^2\) - 40\(x\) + 400 = 625
(\(x-20\))2 = 252
\(\left[{}\begin{matrix}x-20=25\\x-20=-25\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=25+20\\x=-25+20\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=45\\x=-5\end{matrix}\right.\)
\(x=-5\) < 0 (loại)
Vậy \(x=45\)
Kết luận:...