Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, x 2 − 2 ( m + 1 ) x + m 2 + m − 1 = 0 (1)
Với m = 0, phương trình (1) trở thành:
x 2 − 2 x − 1 = 0 Δ ' = 2 ; x 1 , 2 = 1 ± 2
Vậy với m = 2 thì nghiệm của phương trình (1) là x 1 , 2 = 1 ± 2
b) Δ ' = m + 2
Phương trình (1) có hai nghiệm phân biệt ⇔ m > − 2
Áp dụng hệ thức Vi-ét, ta có: x 1 + x 2 = 2 ( m + 1 ) x 1 x 2 = m 2 + m − 1
Do đó:
1 x 1 + 1 x 2 = 4 ⇔ x 1 + x 2 x 1 x 2 = 4 ⇔ 2 ( m + 1 ) m 2 + m − 1 = 4 ⇔ m 2 + m − 1 ≠ 0 m + 1 = 2 ( m 2 + m − 1 ) ⇔ m 2 + m − 1 ≠ 0 2 m 2 + m − 3 = 0 ⇔ m = 1 m = − 3 2
Kết hợp với điều kiện ⇒ m ∈ 1 ; − 3 2 là các giá trị cần tìm.
Đẻ pt 1 có 2 nghiệm pb => \(\Delta,>0\) <=> 1-m+3>0 <=> m<4
Với m<2 thì pt 1 có 2 nghiệm pb x1 x2
=> Theo hệ thức vi ét ta có :
\(\left\{{}\begin{matrix}x1+x2=2< \cdot>\\x1.x2=m-3< \cdot\cdot>\end{matrix}\right.\)
Theo bài ra ta có : x1= 3x2 <=> x1 - 3x2=0 <*>
Từ <*> và <.> ta có hpt
\(\left\{{}\begin{matrix}x1+x2=2\\x1-3x_2=0\end{matrix}\right.\)
Giả ra ta dc: <=>\(\left\{{}\begin{matrix}x1=\dfrac{3}{2}\\x2=\dfrac{1}{2}\end{matrix}\right.\)
Thay x1 và x2 vào <..> ta dc
\(\dfrac{3}{2}.\dfrac{1}{2}=m-3\)
<=> m = \(\dfrac{15}{4}\left(tm\right)\)
Vậy m = ... là giá trị can tìm
Bài làm :
a) Thay m=-5 vào PT ; ta được :
\(x^2-2x-8=0\)
\(\Delta'=\left(-1\right)^2-1.\left(-8\right)=9>0\)
=> PT có 2 nghiệm phân biệt :
\(\hept{\begin{cases}x_1=\frac{1+\sqrt{9}}{1}=4\\x_2=\frac{1-\sqrt{9}}{1}=-2\end{cases}}\)
b) Đk để PT có 2 nghiệm phân biệt :
\(\Delta'>0\Leftrightarrow\left(-1\right)^2-1.\left(m-3\right)=1-m+3=4-m>0\)
\(\Rightarrow m< 4\)
Khi đó ; theo hệ thức Vi-ét ; ta có :
\(\hept{\begin{cases}x_1+x_2=2\left(1\right)\\x_1x_2=m-3\end{cases}}\)
Mà :
\(x_1=3x_2\Rightarrow x_1-3x_2=0\left(2\right)\)
Từ (1) và (2) ; ta có HPT :
\(\hept{\begin{cases}x_1+x_2=2\\x_1-3x_2=0\end{cases}}\Rightarrow\hept{\begin{cases}x_1=\frac{3}{2}\\x_2=\frac{1}{2}\end{cases}}\)
\(\Rightarrow x_1x_2=\frac{3}{4}\Rightarrow m=\frac{3}{4}+3=\frac{15}{4}\left(TMĐK\right)\)
Vậy m=15/4 thì ...
a,x\(^2\)-2x+m-3=0 (*)
thay m=-5 vào pt (*) ta đk:
x\(^2\)-2x+(-5)-3=0⇔x\(^2\)-2x-8=0
Δ=(-2)\(^2\)-4.1.(-8)=36>0
⇒pt có hai nghiệm pb
\(x_1=\dfrac{2+\sqrt{36}}{2}=4\) , \(x_2=\dfrac{2-\sqrt{36}}{2}=-2\)
vậy pt đã cho có tập nghiệm S=\(\left\{4;-2\right\}\)
b,\(x^2-2x+m-3=0\) (*)
Δ=(-2)\(^2\)-4.1.(m-3)=4-4m+12=16-4m
⇒pt luôn có hai nghiệm pb⇔Δ>0⇔16-4m>0⇔16>4m⇔m<4
với m<4 thì pt (*) luôn có hai nghiệm pb \(x_1,x_2\)
theo hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1.x_2=m-3\end{matrix}\right.\) (1) ,(2)
\(x_1,x_2\) TM \(x_1=3x_2\) (3)
từ (1) và (3) ta đk:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2+x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1}{2}\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1}{2}\\x_1=\dfrac{3}{2}\end{matrix}\right.\)
thay \(x_1=\dfrac{3}{2},x_2=\dfrac{1}{2}\) vào (2) ta đk:
\(\dfrac{3}{2}.\dfrac{1}{2}=m-3\Leftrightarrow3=4m-12\Leftrightarrow4m=15\Leftrightarrow m=\dfrac{15}{4}\) (TM)
vậy m=\(\dfrac{15}{4}\) thì pt (*) có hai nghiệm pb \(x_1,x_2\) TMĐK \(x_1=3x_2\)
Do a 2 + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:
Khi đó:
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0
a) Thay m=0 vào phương trình (1), ta được:
\(x^2-2\cdot\left(0-1\right)x+0^2-3m=0\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy: Khi m=0 thì S={0;-2}
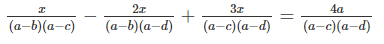
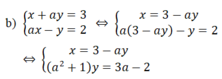
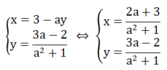
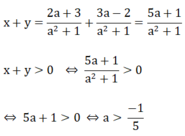
a: \(\left(\dfrac{1}{4\cdot7}+\dfrac{1}{7\cdot10}+...+\dfrac{1}{73\cdot76}\right)\cdot x^2=2\dfrac{16}{19}\)
=>\(\dfrac{1}{3}\left(\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{73\cdot76}\right)\cdot x^2=2+\dfrac{16}{19}=\dfrac{54}{19}\)
=>\(\dfrac{1}{3}\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{73}-\dfrac{1}{76}\right)\cdot x^2=\dfrac{54}{19}\)
=>\(\dfrac{1}{3}\left(\dfrac{1}{4}-\dfrac{1}{76}\right)\cdot x^2=\dfrac{54}{19}\)
=>\(\dfrac{1}{3}\cdot\dfrac{18}{76}\cdot x^2=\dfrac{54}{19}\)
=>\(\dfrac{6}{76}\cdot x^2=\dfrac{54}{19}\)
=>\(x^2=\dfrac{54}{19}:\dfrac{6}{76}=\dfrac{54}{19}\cdot\dfrac{76}{6}=9\cdot4=36\)
=>\(\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
b: \(2^x+2^{x+2}=\dfrac{200}{19}\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{19\cdot20}\right)\)
=>\(2^x+2^x\cdot4=\dfrac{200}{19}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)
=>\(5\cdot2^x=\dfrac{200}{19}\left(1-\dfrac{1}{20}\right)=\dfrac{200}{19}\cdot\dfrac{19}{20}=10\)
=>\(2^x=2\)
=>x=1