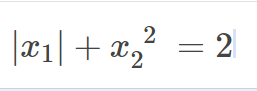
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Phương trình hoành độ giao điểm là: \(x^2-mx+m-1=0\)
\(\Delta=\left(-m\right)^2-4\cdot\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)
Để (P) cắt (d) tại hai điểm phân biệt thì m-2<>0
hay m<>2
b: \(\left|x_A-x_B\right|< 3\)
\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< 3\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2< 9\)
\(\Leftrightarrow m^2-4\left(m-1\right)< 9\)
\(\Leftrightarrow\left(m-2\right)^2-3< 0\)
=>(m+1)(m-5)<0
=>-1<m<5
Xét pt hoành độ gđ của (P) và (d) có:
\(x^2=mx+m+3\)
\(\Leftrightarrow x^2-mx-m-3=0\) (I)
Để (d) cắt (P) tại hai điểm pb ở bên phải trục tung
\(\Leftrightarrow\) Pt (I) có hai nghiệm dương
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S>0\\P>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2+4m+12>0\left(lđ\right)\\m>0\\-m-3>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< -3\end{matrix}\right.\)\(\Rightarrow m\in\varnothing\)
Vậy...
Xét pt hoành độ gđ của parabol và d có:
\(x^2=x+m-1\)
\(\Leftrightarrow x^2-x+1-m=0\) (1)
Để (P) và (d) cắt nhau tại hai điểm pb bên trái trục tung
\(\Leftrightarrow\) Pt (1) có hai nghiệm âm pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S=1< 0\left(vl\right)\\P=1-m>0\end{matrix}\right.\)\(\Rightarrow\) Không tồn tại m để (d) cắt (P) tại hai điểm pb ở bên trái trục tung
Vậy...
Phương trình hoành độ giao điểm là:
\(x^2-x-m+1=0\)
a=1; b=-1; c=-m+1
\(\Delta=b^2-4ac\)
\(=\left(-1\right)^2-4\left(-m+1\right)\)
\(=1+4m-4\)
=4m-3
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow m>\dfrac{3}{4}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-1\right)}{1}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m+1}{1}=-m+1\end{matrix}\right.\)
Để (d) cắt (P) tại hai điểm phân biệt nằm ở bên trái trục tung thì
\(\left\{{}\begin{matrix}m>\dfrac{3}{4}\\x_1+x_2< 0\left(loại\right)\\x_1x_2>0\end{matrix}\right.\)
Vậy: \(m\in\varnothing\)
Pt hoành độ giao điểm:
\(x^2=mx-m+1\Leftrightarrow x^2-mx+m-1=0\) (1)
d cắt (P) tại 2 điểm pb nằm ở 2 phía trục tung khi và chỉ khi (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow1.\left(m-1\right)< 0\)
\(\Leftrightarrow m< 1\)
Đáp án D
Xét phương trình hoành độ giao điểm
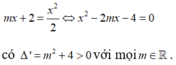
Nên đường thẳng cắt parabol tại hai điểm phân biệt với
a: PTHĐGĐ là:
x^2-2x-|m|-1=0
a*c=-|m|-1<0
=>(d)luôn cắt (P) tại hai điểm phân biệt
b: Bạn bổ sung lại đề đi bạn
1: Tọa độ A là:
y=0 và 4x+m-3=0
=>x=(-m+3)/4 và y=0
=>OA=|m-3|/4
Tọa độ B là:
x=0 và y=m-3
=>OB=|m-3|
Theo đề, ta có: 1/2*(m-3)^2/4=9
=>(m-3)^2/4=18
=>(m-3)^2=72
=>\(m=\pm6\sqrt{2}+3\)
2:
PTHĐGĐ là:
x^2-4x-m+3=0
Δ=(-4)^2-4*(-m+3)=16+4m-12=4m+4
Để (P) cắt (d) tại hai điểm phân biệt thì 4m+4>0
=>m>-1
(4-x1)(x2-1)=2
=>4x2-4-x1x2+1=2
=>x2(x1+x2)-3-(-m+3)=2
=>x2*4-3+m-3=2
=>x2*4=2-m+6=8-m
=>x2=2-1/2m
=>x1=4-2+1/2m=1/2m+2
x1*x2=-m+3
=>-m+3=(1/2m+2)(2-1/2m)=4-1/4m^2
=>-m+3-4+1/4m^2=0
=>1/4m^2-m-1=0
=>m^2-4m-4=0
=>\(m=2\pm2\sqrt{2}\)
Ta có pt hoành độ giao điểm là:
\(-x^2=\left(2-m\right)x+m-3\\ \Leftrightarrow x^2+\left(2-m\right)x+m-3=0\)
Để pt có nghiệm phân biệt thì:
\(\Delta=\left(2-m\right)^2-4\cdot1\cdot\left(m-3\right)\\ =4-4m+m^2-4m+12=m^2-8m+16=\left(m-4\right)^2>0\)
`=>m-4<>0<=>m<>4`
Ta có: `a+b+c=1+(2-m)+(m-3)=0`
\(=>x_1=1\)
Theo vi-ét ta có: \(x_1+x_2=m-2=>x_2=m-2-x_2=m-2-1=m-3\)
\(\left|x_1\right|+x_2^2=2\\ =>1+\left(m-3\right)^2=2\\< =>\left(m-3\right)^2=2-1=1\\ < =>\left[{}\begin{matrix}m-3=1\\m-3=-1\end{matrix}\right.\\ < =>\left[{}\begin{matrix}m=1+3=4\left(ktm\right)\\m=-1+3=2\left(tm\right)\end{matrix}\right.\)
Vậy: ...