B1: Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề:
"∀x ϵ R, ∃y ϵ R, y = x +3"
B2: Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó:
a) ∀n ϵ N: n ⋮ n
b) ∃x ϵ Q: x2 = 2
c) ∀x ϵR: x < x+1
d) ∃x ϵR: 3x = x2 +1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Mệnh đề gốc: Đúng, do $x^2-3x+5=(x-1,5)^2+2,75\geq 2,75>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow x^2-3x+5\neq 0, \forall x\in\mathbb{R}$
Mệnh đề phủ định: $\exists x\in\mathbb{R}, x^2-3x+5=0$

+) Mệnh đề phủ định của mệnh đề P là \(\overline P \): “5,15 không phải là một số hữu tỉ”
Mệnh đề P đúng, \(\overline P \) sai vì \(5,15 = \frac{{103}}{{20}} \in \mathbb{Q}\), là một số hữu tỉ.
+) Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “2 023 không phải là số chẵn” (hoặc “2 023 là số lẻ”)
Mệnh đề Q sai, \(\overline Q \) đúng vì 2 023 có chữ số tận cùng là \(3 \ne \left\{ {0;2;4;6;8} \right\}\), đo đó 2 023 không phải là số chẵn.
P: đúng
phủ định: "5,15 không phải số hữu tỉ"
Q: sai
Phủ định: "1023 không phải số chẵn"

Mệnh đề π < 3, 15 đúng vì π = 3,141592654…
Mệnh đề phủ định: "π ≥ 3, 15"

Mệnh đề ‘’|–125| ≤ 0’’ sai vì |–125| = 125 > 0
Mệnh đề phủ định: "|–125| > 0"

a: Có 1 giá trị x thuộc tập R thỏa mãn x^2=-10
Mệnh đề này sai vì x^2>=0>-10 với mọi x thuộc R
b: Với mọi x thực, x^2+x+12 luôn khác 0
x^2+x+12
=x^2+x+1/4+47/4
=(x+1/2)^2+47/4>=47/4>0 với mọi x
=>Mệnh đề này đúng
c: Với mọi x thuộc R thì x^2 luôn ko lớn hơn 0
Mệnh đề này sai vì ví dụ như x=1 thì 1^2>0 chứ ko bé hơn 0
d: Có một giá trị thực của x thỏa mãn x^2<=0
Mệnh đề này đúng bởi vì có x=0 thỏa mãn x^2<=0
e:
Có một giá trị x thực thỏa mãn x^2+x+5>0
Mệnh đề này đúng vì x^2+x+5=(x+1/2)^2+19/4>0 với mọi x
f: Với mọi giá trị x thực thì x^2+x+5 luôn dương
Mệnh đề này đúng

B: “∃ x ∈ Q : x2 = 2”.
B− : “∀ x ∈ Q : x2 ≠ 2”
B− đúng.
Lưu ý: √2 là số vô tỷ.

C: “∀ x ∈ R : x < x + 1”.
C− : “∃ x ∈ R: x ≥ x + 1”.
C− sai vì x + 1 luôn lớn hơn x.

D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với 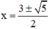
D− thỏa mãn:
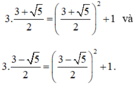
Bài 2:
a) Mệnh đề phủ định là: \("\exists x\in R;n⋮̸n"\)
Mà `n⋮n` với mọi n => Mệnh đề sai
b) Mệnh đề phủ định là: \("\forall x\in Q;x^2\ne2"\)
Ta có: \(x^2\ne2\Leftrightarrow x\ne\pm\sqrt{2}\)
Mà: \(\pm\sqrt{2}\notin Q\) => Mệnh đề đúng
c) Mệnh đề phủ định là: \("\exists x\in R;x\ge x+1"\)
Mà: `x<x+1` với mọi x
`=>` Mệnh đề sai
d) Mệnh đề phủ định là \("\forall x\in R;3x=x^2+1"\)
Ta có: `3x=x^2+1`
`<=>x^2-3x+1=0`
\(\Delta=\left(-3\right)^2-4\cdot1\cdot1=5>0=>\left[{}\begin{matrix}x=\dfrac{3-\sqrt{5}}{2}\\x=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
=> `3x=x^2+1` chỉ đúng với 2 giá trị
=> Mệnh đề sai
Bài 1: "\(\forall x\in R;\exists y\in R;y=x+3\)"
=>Mệnh đề này đúng vì với mọi giá trị của x luôn tồn tại một giá trị của y sao cho y=x+3
Mệnh đề phủ định là: "\(\exists x\in R;\forall y\in R;y\ne x+3\)"