Cho hình thoi ABCD có góc A = 60 độ. Gọi O là giao điểm của 2 đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Chứng minh rằng sáu điểm E, B, F, G, D, H thuộc cùng 1 đường tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

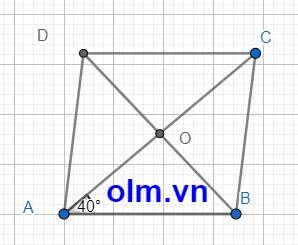
Vì ABCD là hình thoi nên ⇒ tam giác ABD cân tại A
Vì O là trung điểm DB nên AO là truyến là đường phân giác của tam giác ABD
⇒ \(\widehat{DAO}\) = 400
⇒ \(\widehat{DAB}\) = 400 + 400 = 1800
⇒ \(\widehat{ADC}\) = 1800 - 800 = 1000
⇒ \(\widehat{DCB}\) = 1800 - 1000 = 800
\(\Rightarrow\) \(\widehat{ABC}\) = 1800 - 800 = 1000

Vì ABCD là hình thoi nên \(AB=BC=CD=DA=20\left(cm\right)\)
Và AC cắt BD tại O nên O là trung điểm AC,BD
\(\Rightarrow AC=2AO=32\left(cm\right);BD=2OB=24\left(cm\right)\)

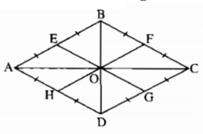
Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).
O A E B F C G H D
Đặt OB = OD = a. Hãy chứng minh OE = a
Tương tự, OF = OG = OH = a
Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn ( O;a )
Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
Ta có: ΔDAB cân tại D
mà DE là đường trung tuyến
nên DE vuông góc với BE
=>E nằm trên đường tròn đường kính BD(1)
Ta có:ΔBAD cân tại B
ma BH là đường trung tuyến
nên BH vuông góc với HD
=>H nằm trên đường tròn đường kính BD(2)
Xét ΔCBD có CB=CD và góc BCD=60 độ
nên ΔCBD đều
Ta có: ΔBDC cân tại D
mà DF là đường trung tuyến
nen DF vuông góc với BF
=>F nằm trên đường tròn đường kính BD(3)
Ta có: ΔBDC cân tại B
mà BG là đường trung tuyến
nên BG vuông góc với GD
=>G nằm trên đường tròn đường kính BD(4)
Từ (1), (2), (3) và (4) suy ra E,B,F,G,D,H cùng nằm trên 1 đường tròn