cho tam giác ABC có B = 60 độ C = 30 độ .tia phân giác của góc A cắt BC tại D. kẻ AH vuông góc với BC (H thuộc BC). a) tính số đo của BAC ADH HAD b) kẻ DE //AB chứng minh EK vuông góc AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. -△AEC và △ADB có: \(\widehat{AEC}=\widehat{ADB}=90^0;\widehat{BAC}\) là góc chung.
\(\Rightarrow\)△AEC∼△ADB (g-g).
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AC}{AB}\Rightarrow AE.AB=AD.AC\).
\(\Rightarrow\dfrac{AE}{AC}=\dfrac{AD}{AB}\)
b. -△ADE và △ABC có: \(\dfrac{AE}{AC}=\dfrac{AD}{AB};\widehat{BAC}\) là góc chung.
\(\Rightarrow\)△ADE∼△ABC (g-g).
c. -△AEC vuông tại E có: \(\widehat{EAC}=60^0\Rightarrow AE=\dfrac{AC}{2}\)
-△ADE∼△ABC \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AE}{AC}\right)^2=\dfrac{1}{4}\)
\(\Rightarrow S_{ADE}=\dfrac{1}{4}S_{ABC}=\dfrac{1}{4}.120=30\left(cm^2\right)\)
C/m \(AE=\dfrac{AC}{2}\):
-Lấy M là trung điểm BC.
-△AEC vuông tại E có: EM là trung tuyến.
\(\Rightarrow AM=EM=\dfrac{1}{2}AC\)
\(\Rightarrow\)△AEM cân tại M mà \(\widehat{EAM}=60^0\).
\(\Rightarrow\)△AEM đều \(\Rightarrow AE=AM=\dfrac{AC}{2}\)

Khó king khủng em mới học lớp 4 thôi để em ăn cháo sen bát bảo minh trung làm được ngay nhưng phải làm thêm tí bò húc với lại rượu đế ! la la la la la ta là một con người

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: góc A=90-30=60 độ
ΔADE đồng dạng với ΔABC
=>S ADE/S ABC=(AD/AB)^2=1/4
=>S ABC=120cm2

1b) Tam giác AMN vuông tại M có góc A = 600 => góc N = 300
Tam giác vuông AMD và tam giác vuông NMA có góc A = góc N(cùng = 300) nên chúng đồng dạng
=> SAMD/SNMA = (AM/MN)2 = AM2/MN2 (1)
Gọi I là trung điểm của AN => MI là trung tuyến tg AMN vuông tại M => MI = IA = 1/2AN => tg AMI cân tại I mà góc A = 600
=> tg AMI đều => AM = AI = 1/2AN
Theo Pytago ta có AN2 = AM2 + MN2 => (2AM)2 - AM2 =MN2 => 3AM2 = MN2 => AM2/MN2 = 1/3 (2)
Từ (1) và (2) bn suy ra nhé
1b) Tam giác AMN vuông tại M có góc A = 60o
Tam giác vuông AMD và tam giác vuông NMA có góc A = góc N(cùng = 30o) nên chúng đồng dạng
=> SAMD/SNMA = (AM/MN)2 = AM2 /MN2 (1)
Gọi I là trung điểm của AN => MI là trung tuyến tg AMN vuông tại M => MI = IA = 1/2AN => tg AMI cân tại I mà góc A = 60o
=> tg AMI đều => AM = AI = 1/2AN
Từ (1) và (2) bn suy ra nhé

30 o N B C M A 10
a. Trong tam giác vuông ABC, ta có :
\(AB=BC.\sin\widehat{C}=10.\sin30^o=10.\frac{1}{2}=5\left(cm\right)\)
\(AC=BC.\cos\widehat{C}=10.\cos30^o=10.\frac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
b)
Ta có : \(BM\perp BN\)( tính chất 2 góc kề bù ) \(\Rightarrow\widehat{MBN}=90^o\left(1\right)\)
\(AM\perp BM\left(gt\right)\Rightarrow\widehat{AMB}=90^o\left(2\right)\)
\(AN\perp BN\left(gt\right)\Rightarrow\widehat{ANB}=90^o\left(3\right)\)
Từ (1) (2) và (3) , suy ra : tứ giác AMBN là hình chữ nhật
\(\Rightarrow\Delta AMB=\Delta NBM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{NMB}\)
Mà \(\widehat{ABM}=\widehat{MBC}\left(gt\right)\)
\(\Rightarrow\widehat{NMB}=\widehat{NBC}\)
Suy ra: MN // BC (có cặp góc so le trong bằng nhau)
Vì AMBN là hình chữ nhật nên AB = MN
)): gửi cả câu c) rồi mà cuối cùng lại 0 có , làm lại câu c) sang bên này :>
c)
Tam giác ABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
\(\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{ABM}=\frac{1}{2}\widehat{B}=\frac{1}{2}.60^o=30^o\)
Xét 2 tam giác ABC và MAB ,, ta có :
\(\widehat{BAC}=\widehat{AMB}=90^o\)
\(\widehat{ACB}=\widehat{ABM}=90^o\)
\(\Rightarrow\Delta ABC~\Delta MAB\left(g.g\right)\)
=> Tỉ số đồng dạnh \(k=\frac{AB}{BC}=\frac{5}{10}=\frac{1}{2}\)

a: Xét ΔOKB vuông tại K và ΔOHC vuông tại H co
góc KOB=góc HOC
=>ΔOKB đồng dạng với ΔOHC
d: góc BKC=góc BHC=90 độ
=>BKHC nộitiếp
=>góc AKH=góc ACB
=>ΔAKH đồng dạng với ΔACB
=>\(\dfrac{S_{AKH}}{S_{ACB}}=\left(\dfrac{AK}{AC}\right)^2=\dfrac{1}{4}\)
=>\(S_{ABC}=32\left(cm^2\right)\)

a) Xét tam giác ADB vuông tại D
tam giác AEC vuông tại E
có A góc chung
=>tam giác ADB đồng dạng tam giác AEC (g-g)
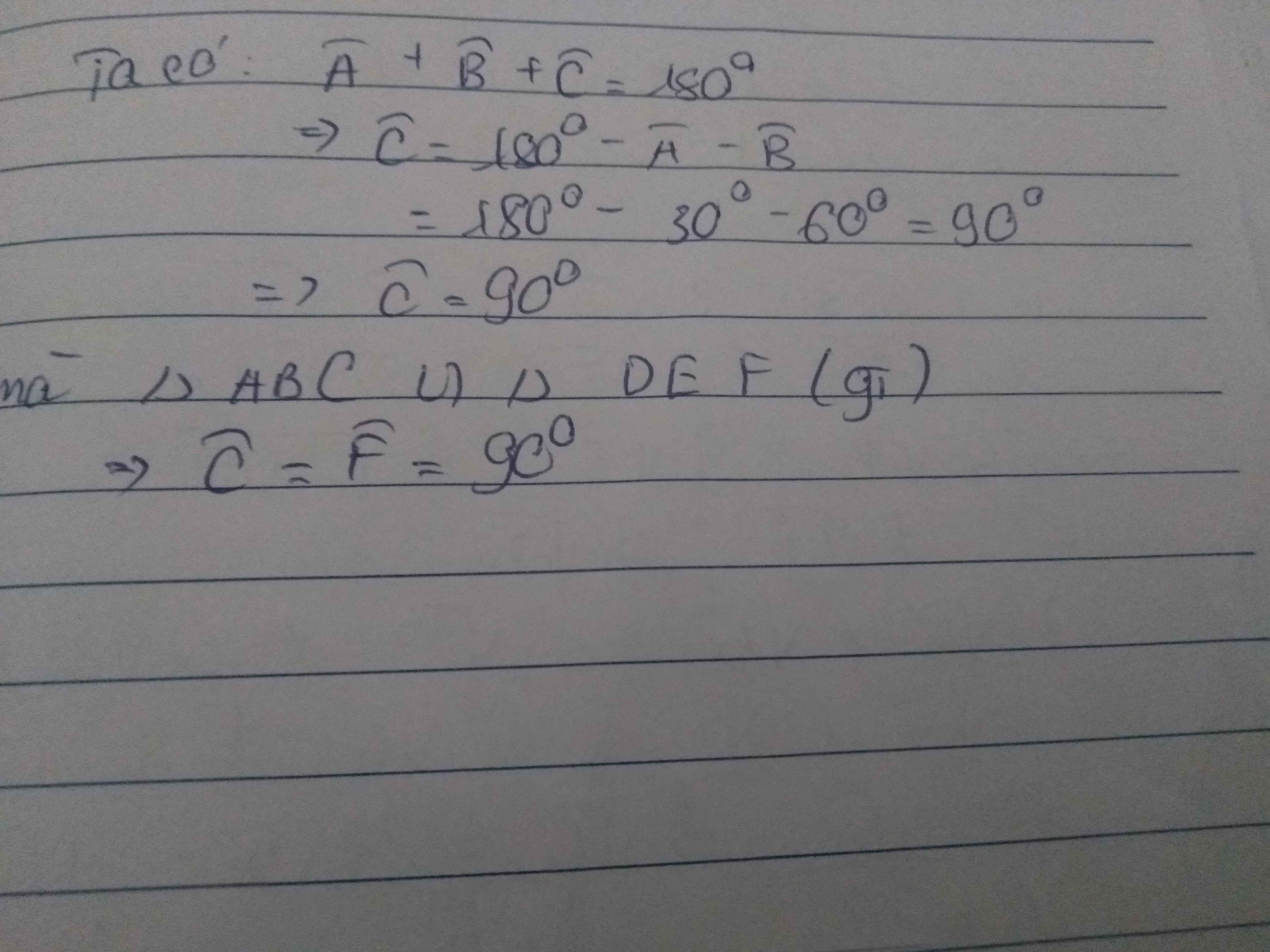
a: Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAC}+60^0+30^0=180^0\)
=>\(\widehat{BAC}=90^0\)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=45^0\)
Ta có: \(\widehat{BAH}+\widehat{B}=90^0\)(ΔBHA vuông tại H)
=>\(\widehat{BAH}=90^0-60^0=30^0\)
Vì \(\widehat{BAH}< \widehat{BAD}\)
nên tia AH nằm giữa hai tia AB và AD
=>\(\widehat{BAH}+\widehat{HAD}=\widehat{BAD}\)
=>\(\widehat{HAD}=45^0-30^0=15^0\)
ΔAHD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HDA}=90^0-15^0=75^0\)