Chứng tỏ rằng:
\(\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}+\dfrac{3}{15}+\dfrac{3}{16}+\dfrac{3}{17}+\dfrac{3}{18}< \dfrac{7}{4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có BĐT cô si:\(a+b\ge2\sqrt{ab}\)(1)
Mặt khác a,b là các số âm nên a+b<0 mà \(2\sqrt{ab}>0\)
\(\Rightarrow a+b< 2\sqrt{ab}\left(2\right)\)
Từ (1) và (2) suy ra vô lý
vậy...............

Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.

Ta có : \(\left(a-b\right)^2\ge0\)
\(\Rightarrow a^2+b^2+2ab\ge4ab\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
Có : \(a,b\ge0\)
\(\Rightarrow a+b\ge2\sqrt{ab}\)
\(\Leftrightarrow\dfrac{a+b}{2}\ge\sqrt{ab}\) ( đpcm )
Vậy ...

2n + 1 > 2n + 3 (2)
+ Với n = 2 thì (2) ⇔ 8 > 7 (luôn đúng).
+ Giả sử (2) đúng khi n = k ≥ 2, nghĩa là 2k+1 > 2k + 3.
Ta chứng minh đúng với n= k+ 1 tức là chứng minh: 2k+2 > 2(k+ 1)+ 3
Thật vậy, ta có:
2k + 2 = 2.2k + 1
> 2.(2k + 3) = 4k + 6 = 2k + 2 + 2k + 4.
> 2k + 2 + 3 = 2.(k + 1) + 3 ( Vì 2k + 4 >3 với mọi k ≥ 2)
⇒ (2) đúng với n = k + 1.
Vậy 2n + 1 > 2n + 3 với mọi n ≥ 2.

Vì a ≥ 0 nên √a xác định, b ≥ 0 nên b xác định
Ta có: a - b 2 ≥ 0 ⇔ a - 2 a b + b ≥ 0
⇒ a + b ≥ 2 a b ⇔ a + b 2 ≥ a b
Dấu đẳng thức xảy ra khi a = b.

Bạn tham khảo cách chứng minh tại đây :
Câu hỏi của Nguyễn Huy Thắng - Toán lớp 10 | Học trực tuyến
Áp dụng : Theo BĐT \(AM-GM\) ta có :
\(a+b+c\ge3\sqrt[3]{abc}\)
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3\sqrt[3]{\dfrac{1}{abc}}\)
Nhân vế theo vế ta được :
\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\dfrac{1}{abc}}=3.3.1=9\)
Dấu \("="\) xảy ra khi \(a=b=c\)

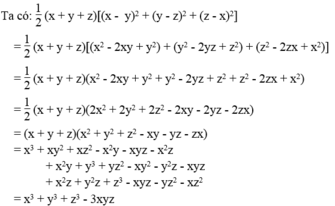
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
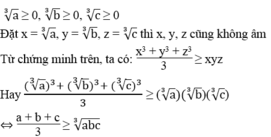
Ta có:
\(\dfrac{3}{12}=\dfrac{3}{12}=1\)
\(\dfrac{3}{13}< \dfrac{3}{12}\)
\(\dfrac{3}{14}< \dfrac{3}{12}\)
\(\dfrac{3}{15}< \dfrac{3}{12}\)
\(\dfrac{3}{16}< \dfrac{3}{12}\)
\(\dfrac{3}{17}< \dfrac{3}{12}\)
\(\dfrac{3}{18}< \dfrac{3}{12}\)
\(\rightarrow\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}+\dfrac{3}{15}+\dfrac{3}{16}+\dfrac{3}{17}+\dfrac{3}{18}< \dfrac{3}{12}+\dfrac{3}{12}+\dfrac{3}{12}+\dfrac{3}{12}+\dfrac{3}{12}+\dfrac{3}{12}+\dfrac{3}{12}=\dfrac{3+3+3+3+3+3+3}{12}=\dfrac{21}{12}=\dfrac{7}{4}\)Vậy: \(\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}+\dfrac{3}{15}+\dfrac{3}{16}+\dfrac{3}{17}+\dfrac{3}{18}< \dfrac{7}{4}\)