Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vẽ tia AG là tia đối của tia AC
Ta có: \(\widehat{FAB}=\widehat{ABC}\)(hai góc so le trong, AF//BC)
\(\widehat{GAF}=\widehat{ACB}\)(hai góc đồng vị, AF//BC)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{BAF}=\widehat{GAF}\)
hay Ax là tia phân giác của góc ngoài tại đỉnh A(đpcm)
a. Vì Ay // BC => góc yAC = góc ACB (sole trong)
góc yAx = góc ABC (đòng vị)
Mà góc ABC = góc ACB => góc yAC = góc yAx => Ay là phân giác góc CAx
b. Vì AD là phân giác góc trong BAC , Ay là phân giác góc ngoài CAx
=> Ay vuông góc với AD ( tính chất phân giác trong và ngoài )
Mà Ay // BC => góc yAD = góc ADB ( sole trong) => AD vuông góc với BC
#HT#
a:
b:
BD//AC
=>\(\widehat{DBA}=\widehat{BAC}\)(hai góc so le trong)(1)
CB//AD
=>\(\widehat{CBA}=\widehat{DAB}\)(hai góc so le trong)(2)
AB là phân giác của góc CAD
=>\(\widehat{CAB}=\widehat{DAB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{DBA}=\widehat{CBA}\)
Xét ΔACB và ΔADB có
\(\widehat{DBA}=\widehat{CBA}\)
BA chung
\(\widehat{CAB}=\widehat{DAB}\)
Do đó: ΔACB=ΔADB
=>AC=AD và BC=BD
c: Xét ΔAHB vuông tại H và ΔAKB vuông tại K có
AB chung
\(\widehat{HAB}=\widehat{KAB}\)
Do đó: ΔAHB=ΔAKB
=>BH=BK
d: Xét tứ giác AHBK có
\(\widehat{AHB}+\widehat{AKB}+\widehat{KAH}+\widehat{KBH}=360^0\)
=>\(\widehat{KBH}+60^0+90^0+90^0=360^0\)
=>\(\widehat{KBH}=360^0-90^0-90^0-60^0=120^0\)
Giải :a) Ta có BD // Ay (gt)
=> góc DBM = góc A (so le trong)
mà góc A = 900 => góc BDM = 900
Xét tam giác AMC và tam giác BMD
có góc A = góc DBM = 900 (cmt)
MA = MB(gt)
góc AMC = góc BMD ( đối đỉnh)
=> tam giác AMC = tam giác BMD (g.c.g)
b) Ta có : tam giác AMC = tam giác BMD (cm câu a)
=> MC = MD ( hai cạnh tương ứng)
Xét tam giác MEC và tam giác MED
có MC = MD (cmt)
CME = DME (gt)
ME : chung
=> tam giác MEC = tam giác MED (c.g.c)
=> góc CEM = góc DEM (hai góc tương ứng)
Mà tia EM nằm giữa ED và EC
=> EM là tia p/giác của góc DEC (Đpcm)
c) Ta có : tam giác AMC = tam giác BMD (cm câu a)
=> BD = AC ( hai cạnh tương ứng)
Mà DE = BD + BE
hay AC + BE = DE
=> BE = DE - AC (1)
Ta lại có tam giác MEC = tam giác MED (cm câu b)
=> EC = ED (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra BE = CE - AC (Đpcm)
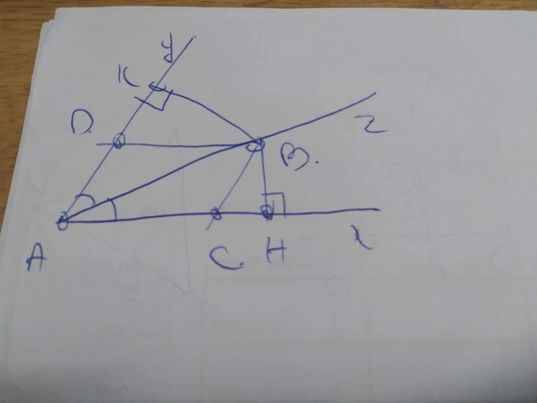
Ta có:
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}=180^o-40^o-40^o=100^o\)
Vì Ax là phân giác ngoài \(\widehat{A}\)
\(\Rightarrow\widehat{CAM}=\frac{180^o-\widehat{BAC}}{2}=\frac{180^o-100^o}{2}=40^o\)
\(\Rightarrow\widehat{CAM}=\widehat{BCA}=40^o\)
\(\Rightarrow\)BC // Ax (so le trong)
Vì Ay là phân giác trong \(\widehat{A}\)
\(\Rightarrow\widehat{NAC}=\frac{100^o}{2}=50^o\)
\(\Rightarrow\widehat{NAC}+\widehat{CAM}=50^o+40^o=90^o\)
\(\Rightarrow AM\perp AN\)
b/ Ta có:
\(\widehat{NAM}=\widehat{AKM}=90^o\)
\(\Rightarrow\widehat{MAK}=180^o-\widehat{AKM}-\widehat{AMK}=90^o-\widehat{AMK}=\widehat{MNA}\)
c/ Tương tự câu b