Giúp mik nhe
Cho tam giác ABC vuông tại A, đường cao AH. Tia phân giác của góc BAH cắt BH tại D. Chứng minh rằng:
a) góc ABH = góc HAC
b) góc ADC = góc DAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 3 2021
a) Xét ΔAMN và ΔAMP có
MA chung
\(\widehat{NMA}=\widehat{PMA}\)(MA là tia phân giác của \(\widehat{NMP}\))
MN=MP(ΔMNP cân tại M)
Do đó: ΔAMN=ΔAMP(C-g-c)
18 tháng 11 2021
Xét tam giác OCB: \(\widehat{OBC}+\widehat{OCB}=180^0-\widehat{BOC}=45^0\)
Mà OB,OC là p/g nên \(\widehat{OBC}+\widehat{OCB}=\dfrac{1}{2}\widehat{ABC}+\dfrac{1}{2}\widehat{ACB}=\dfrac{1}{2}\left(\widehat{ACB}+\widehat{ABC}\right)\)
\(\Rightarrow\widehat{ACB}+\widehat{ABC}=90^0\)
Xét tam giác ABC: \(\widehat{BAC}=180^0-\widehat{ACB}-\widehat{ABC}=180^0-\left(\widehat{ACB}+\widehat{ABC}\right)=90^0\)
Vậy ABC vuông tại A
KV
24 tháng 12 2023
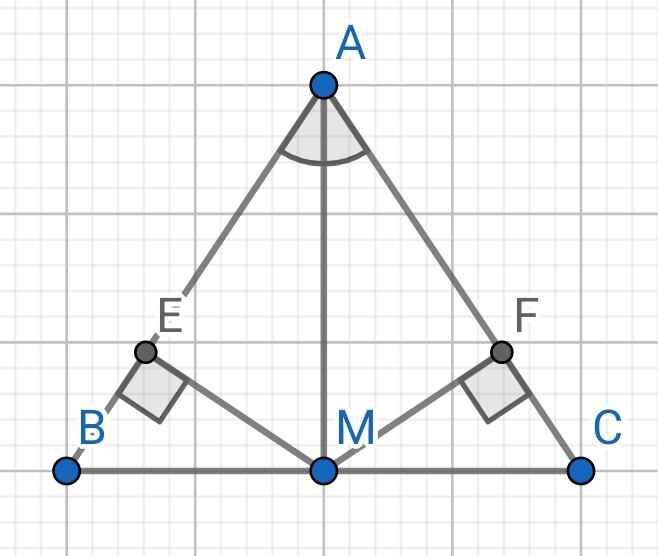a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
P
24 tháng 12 2023
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)
LB
24 tháng 12 2023
Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):
a, Chứng minh △ABM = △ACM.
b, Chứng minh M là trung điểm của BC và AM ⊥ BC.
c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.
Giải:
a,
- Xét 2 △ABM và △ACM, có:
AB = AC (theo giả thiết)
∠CAM = ∠BAM (AM là phân giác của ∠BAC)
AM_cạnh chung
=> △ABM = △ACM (c.g.c)
b,
- Có △ABM = △ACM (chứng minh trên)
=> MC = MB (2 cạnh tương ứng)
=> M là trung điểm của BC
=> ∠AMC = ∠AMB (2 góc tương ứng)
mà 2 ∠AMC và ∠AMB kề bù
=> ∠AMC = ∠AMB = \(\dfrac{180^o}{2}\) = 90o
<=> AM ⊥ BC
c,
- Xét 2 △AEM và △AFM, có:
∠AEM = ∠AFM = 90o
AM_cạnh chung
∠EAM = ∠FAM (AM là phân giác của ∠EAF)
=> △AEM = △AFM (cạnh huyền - góc nhọn)
=> AE = AF (2 cạnh tương ứng)
<=> △AEF cân tại A
=> ∠AEF = \(\dfrac{180^o-\text{∠}EAF}{2}\) (số đo của một góc ở đáy trong △AEF cân tại A) (1)
Có △ABC cân tại A (AB = AC)
=> ∠ACB = \(\dfrac{180^o-\text{∠}BAC}{2}\) (số đo của một góc ở đáy trong ΔABC cân tại A) (2)
Từ (1) và (2) suy ra ∠AEF = ∠ACB
mà ∠AEF và ∠ACB ở vị trí đồng vị
=> EF//BC
10 tháng 4 2022
a: Xét ΔBAK có
BE là đường cao
BE là đường trung tuyến
Do đó: ΔBAK cân tại B
b: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)
a: \(\widehat{ABH}+\widehat{HAB}=90^0\)(ΔAHB vuông tại H)
\(\widehat{HAB}+\widehat{HAC}=\widehat{BAC}=90^0\)
Do đó: \(\widehat{ABH}=\widehat{HAC}\)
b: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{CDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{HAD}\)(AD là phân giác của góc BAH)
nên \(\widehat{CAD}=\widehat{CDA}\)