Cho hình thang MNPQ (MN//PQ) Gọi I là trung điểm MQ ,IK //MN . Tính độ dài IK biết MN =4cm , PQ=7cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 11 2021
có:
\(\dfrac{18+MN}{2}=16,5\Leftrightarrow18+MN=33\Leftrightarrow MN=15\)
like cho mk nha
2 tháng 10 2021
a: Xét hình thang MNPQ có
I là trung điểm của MQ
IK//MN//QP
Do đó: K là trung điểm của NP
b: Xét hình thang MNPQ có
I là trung điểm của MQ
K là trung điểm của NP
Do đó: IK là đường trung bình của hình thang MNPQ
Suy ra: \(IK=\dfrac{MN+PQ}{2}=6.5\left(cm\right)\)
24 tháng 10 2021
a: Xét hình thang MNPQ có
I là trung điểm của MQ
K là trung điểm của NP
Do đó: IK là đường trung bình của hình thang MNPQ
Suy ra: \(IK=\dfrac{MN+QP}{2}=10\left(cm\right)\)
5 tháng 10 2021
a: Xét hình thang MNPQ có
A là trung điểm của MQ
B là trung điểm của NP
Do đó: AB là đường trung bình của hình thang MNPQ
Suy ra: AB//MN//PQ
Xét ΔQMN có AI//MN
nên \(\dfrac{AI}{MN}=\dfrac{AQ}{QM}=\dfrac{1}{2}\left(1\right)\)
Xét ΔPMN có KB//MN
nên \(\dfrac{KB}{MN}=\dfrac{1}{2}\left(2\right)\)
Từ (1) và (2) suy ra AI=KB
25 tháng 7 2023
1: Xét ΔNMP có NA/NM=NB/NP
nên AB//MP và AB=MP/2
Xét ΔQMP có QC/QP=QD/QM
nên DC//MP và DC=MP/2
=>AB//DC và AB=DC
=>ABCD là hình bình hành
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 7 2023
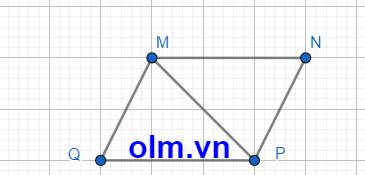
Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
\(\widehat{QPM}\) = \(\widehat{PMN}\) (2 góc so le trong)
\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)
\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)
\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)
b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
MN = PQ
\(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)
⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)
\(\Rightarrow\) MQ = NP (đpcm)
⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\)
Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:
QM // NP (đpcm)
Xét hình thang MNPQ có:
MI=MQ
IK//MN
=> KN=KP
=> IK là đường trung bình
=> IK=(MN+PQ)/2
=(4+7)2
=5,5(cm)
IK // MN
MN // PQ
suy ra: IK // MN // PQ
mà I là trung điểm MQ
nên K là trung điểm NP
\(\Rightarrow\)IK là đường trung bình của hình thang MNPQ
\(\Rightarrow\)IK = \(\frac{MN+PQ}{2}\)= \(\frac{4+7}{2}\)= 5,5