Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công thức tính thể tích hình lập phương cạnh a là:
V= a.a.a = \({a^3}\)
Bài toán mở đầu:
Biểu thức lũy thừa tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilomét khối) là:
V =\({(1111,34)^3}\)

a) Ta có: M(x) = 5x3 + 2x4 – x2 + 3x2 – x3 – x4 + 1 – 4x3 = x4 + 2x2 + 1 b) Ta có (M1) = 14 + 2.12 + 1 = 1 + 2 + 1 = 4 và (M-1) = (-1)4 + 2.(-1)2 + 1 + 1 + 2 + 1 = 4 c) Ta có M(x) = x4 + 2x2 + 1 = (x2+1)2 Nhận xét: Vì x2 ≥ 0 => x2 + 1 > 1 => (x2 + 1)2 > 1 > 0 với mọi x ∈ R Vậy M(x) = (x2 +1)2 > 0 với mọi x ∈ R. Điều này chứng tỏ rằng M(x) không có nghiệm trong R.
Bạn ơi phần nào có số đằng sau x là mũ nhé! ko biết ấn dấu mũ

1: \(A\left(x\right)=-3x^3+4x^2+4x+3\)
\(B\left(x\right)=-3x^3+4x^2-x+7\)
2: \(A-B=0\)
=>4x+3-x+7=0
=>3x+10=0
hay x=-10/3
1)
\(A=9-x^3+4x-2x^3+4x^2-6\)
\(A=(9-6)+\left(-x^3-2x^3\right)+4x+4x^2\)
\(A=3-3x^3+4x+4x^2\)
\(A=-3x^3+4x^2+4x+3\)
\(B=3+x^3+4x^2+2x^3+7x-6x^3-8x+4\)
\(B=(3+4)+(x^3+2x^3-6x^3)+4x^2+(7x-8x)\)
\(B=7-3x^3+4x^2-x\)
\(B=-3x^3+4x^2-x+7\)
2) \(A-B=(-3x^3+4x^2+4x+3)-\) \((-3x^3+4x^2-x+7)\)
\(A-B=-3x^3+4x^2+4x+3+\)\(3x^3-4x^2+x-7\)
\(A-B\) \(=\left(-3x^3+3x^3\right)+\left(4x^2-4x^2\right)+\left(4x+x\right)+\left(3-7\right)\)
\(A-B\) \(=5x-4\)
Đặt tên cho đa thức \(5x-4\) là \(H\left(x\right)\)
Cho \(H\left(x\right)=0\)
hay \(5x-4=0\)
\(5x\) \(=0+4\)
\(5x\) \(=4\)
\(x\) \(=4:5\)
\(x\) \(=\) \(0,8\)
Vậy \(x=0,8\) không phải là nghiệm của H(\(x\))
MIK KHÔNG CHẮC LÀ CÂU 2 ĐÚNG

Đa thức biểu thị kết quả thứ nhất: K = (x + 1)2
Đa thức biểu thị kết quả thứ hai: H = (x – 1)2
Đa thức biểu thị kết quả cuối cùng:
Q = K – H = (x + 1)2 - (x – 1)2
= (x+1).(x+1) - (x – 1). (x – 1)
= x.(x+1) + 1.(x+1) - x(x-1) + (-1). (x-1)
= x.x + x.1 + 1.x + 1.1 –[ x.x – x .1 + (-1).x + (-1) . (-1)]
= x2 + x + x + 1 – (x2 – x – x + 1)
= x2 + x + x + 1 – x2 + x + x – 1
= (x2 - x2 ) + (x+x+x+x) + (1- 1)
= 4x
Để tìm x, ta lấy kết quả cuối cùng chia cho 4

a, \(P\left(x\right)=5x^5-4x^2+7x+1;Q\left(x\right)=5x^5-4x^2+3x+8\)
b, \(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c, \(P\left(x\right)=Q\left(x\right)\Rightarrow7x+1=3x+8\Leftrightarrow4x=7\Leftrightarrow x=\dfrac{7}{4}\)
a/ \(P\left(x\right)=8x^5+7x-6x^2-3x^5+2x^2+1\)
\(=8x^5-3x^5-6x^2+2x^2+7x+1\)
\(=5x^5-4x^2+7x+1\)
\(Q\left(x\right)=4x^5+3x-2x^2+x^5-2x^2+8\)
\(=4x^5+x^5-2x^2-2x^2+3x+8\)
\(=5x^5-4x^2+3x+8\)
b/ \(P\left(x\right)=5x^5-4x^2+7x+1\)
+ \(Q\left(x\right)=5x^5-4x^2+3x+8\)
____________________________
\(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c/ \(P\left(x\right)=Q\left(x\right)\)
\(\Rightarrow5x^5-4x^2+7x+1=5x^5-4x^2+3x+8\)
\(\Rightarrow7x+1=3x+8\)
\(\Rightarrow4x-7=0\)
\(\Rightarrow x=\dfrac{7}{4}\)
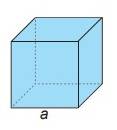
\(c,C=4^{100}-4^{98}-4^{96}-...-1\\ C=4^{100}-\left(1+4^2+...+4^{98}\right)\)
Đặt: `D=1+4^2+...+4^98`
`4^2D=4^2+4^4+...+4^100`
`16D-D=(4^2+4^4+...+4^100)-(1+4^2+...+4^98)`
`15D=4^100-1`
`D=(4^100-1)/15`
\(C=4^{100}-\dfrac{4^{100}-1}{15}=\dfrac{15\cdot4^{100}-4^{100}+1}{15}=\dfrac{14\cdot4^{100}+1}{15}\)
\(d,D=3^{100}-3^{99}+3^{98}-...-3+1\\ D=3^{100}-\left(3^{99}-3^{98}+...+3-1\right)\)
Đặt: `S=3^99-3^98+....+3-1`
`3S=3^100-3^99+...+3^2-3`
`3S+S=(3^100+3^99+...+3^2-3)+(3^99-3^98+3-1)`
`4S=3^100-1`
`S=(3^100-1)/4`
\(D=3^{100}-\dfrac{3^{100}-1}{4}=\dfrac{4\cdot3^{100}-3^{100}+1}{4}=\dfrac{3^{101}+1}{4}\)
ai giúp mik giải bài này vs