tìm min của D=\(^{x^2-2xy+6y^2-12x+2y+45}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
3 tháng 2
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
AH
Akai Haruma
Giáo viên
3 tháng 2
Câu 2:
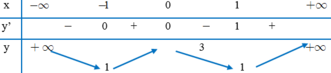
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
CM
26 tháng 8 2017
+ Ta có đạo hàm : y= 3x2- 3 và y’ =0 khi và chỉ khi x= 1 hoặc x= -1 .
+ Hàm số đồng biến trên khoảng ( 1; + ∞) .
+ Trên D= [m+1; m+ 2], với m> 0 ,
ta có : M i n [ m + 1 ; m + 2 ] y = ( m + 1 ) 3 - 3 ( m + 1 ) + 1
Ycbt min y< 3 hay m3+ 3m2-4< 0
Suy ra ( m-1) (m+ 2) 2) < 0
Khi đó; m< 1 và m≠- 2
+ Kết hợp điều kiện . Suy ra: 0< m< 1.
Chọn A.
KN
4 tháng 7 2019
\(C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\)
Ta có: \(\left|x+\frac{4}{7}\right|\ge0\)nên \(-\left|x+\frac{4}{7}\right|\le0\)
\(\Rightarrow C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\le\frac{12}{19}\)
\(\Rightarrow C_{max}=\frac{12}{19}\)
(Dấu "="\(\Leftrightarrow x=\frac{-4}{7}\))
KN
4 tháng 7 2019
\(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\)
Vì \(\left|x-\frac{5}{7}\right|\ge0\)nên \(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\ge\frac{2}{3}\)
\(\Rightarrow D_{min}=\frac{2}{3}\)
(Dấu "="\(\Leftrightarrow x=\frac{5}{7}\))
CM
31 tháng 7 2017
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
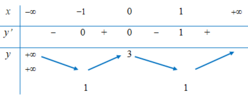
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
CM
9 tháng 2 2019
Ta có y = x 2 + 2 x + a - 4 = x + 1 2 + a - 5
Đặt u = x + 1 2 khi đó ∀ x ∈ - 2 ; 1 thì u ∈ 0 ; 4
Ta được hàm số f u = u + a - 5
Khi đó
M a x x ∈ - 2 ; 1 y = M a x x ∈ 0 ; 4 f u = M a x f 0 , f 4 = M a x a - 5 ; a - 1
Trường hợp 1:
a - 5 ≤ a - 1 ⇔ a ≤ 3 ⇒ M a x x ∈ 0 ; 4 f u = 5 - a ≥ 2 ⇔ a = 3
Trường hợp 2:
a - 5 ≤ a - 1 ⇔ a ≥ 3 ⇒ M a x x ∈ 0 ; 4 f u = a - 1 ≥ 2 ⇔ a = 3
Vậy giá trị nhỏ nhất của M a x x ∈ - 2 ; 1 y = 2 ⇔ a = 3
Đáp án A
24 tháng 9 2023
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
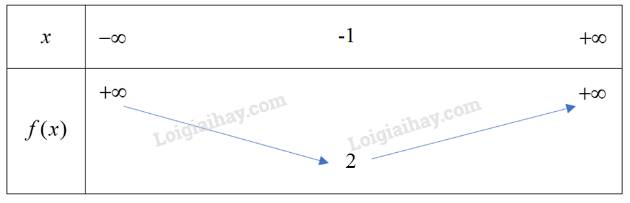
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
CM
30 tháng 4 2018
Đáp án D.
Sử dụng máy tính cầm tay chức năng TABLE với thiết lập Start ‒5; End 5; Step 1 thì ta có
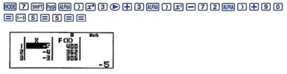
Từ bảng giá trị ta kết luận được giá trị lớn nhất của hàm số đạt được là 400 khi x = − 5 .
Từ bảng giá trị trên ta chưa thể kết luận được giá trị nhỏ nhất của hàm số.
Ta thấy x 3 + 3 x 2 − 72 x + 90 ≥ 0, ∀ x ∈ ℝ .
Dấu bằng xảy ra khi x 3 + 3 x 2 − 72 x + 90 = 0 .
Trong ba nghiệm trên ta thấy nghiệm x 3 ∈ − 5 ; 5 . Từ đây ta có thể kết luận giá trị nhỏ nhất của hàm số đạt được là 0 khi x = x 3 .
Vậy tổng cần tìm là 400. Ta chọn D.
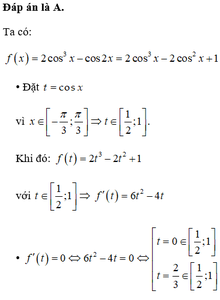
\(D=\left(x^2-2xy+y^2\right)-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y\right)^2-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y-6\right)^2+5y^2+9\)
Do \(\left\{{}\begin{matrix}\left(x-y-6\right)^2\ge0\\5y^2\ge0\end{matrix}\right.\) ;\(\forall x;y\)
\(\Rightarrow D\ge9\)
\(D_{min}=9\) khi \(\left\{{}\begin{matrix}x-y-6=0\\5y^2=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(6;0\right)\)