
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

a: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
b: Vì ABCD là hình bình hành
nên AC và BD cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của BD
hay B và D đối xứng nhau qua O

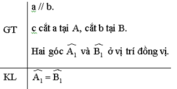
Chứng minh
Giả sử ∠(A1) ≠ ∠(B1)
Qua B kẻ đường thẳng xy sao cho ∠(ABy) = ∠(A1)
Mà hai góc này ở vị trí so le trong nên theo dấu hiệu của hai đường thẳng song song, ta có xy //a
+) Qua điểm B ta kẻ được hai đường thẳng b và xy cùng song song với đường thẳng a. Theo tiên đề Ơ- clit suy ra đường thẳng xy trùng với đường thẳng b.
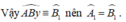

6:
a: Xét ΔABC và ΔCDA có
góc BAC=góc DCA
AC chung
góc BCA=góc DAC
=>ΔABC=ΔCDA
b: Xét ΔADB và ΔCBD có
AD=CB
AB=CD
DB chung
=>ΔADB=ΔCBD
c: Xét tứ giác ABCD có
AB//CD
AD//BC
=>ABCD là hình bình hành
=>O là trung điểm chung của AC và DB
Xét ΔOAB và ΔOCD có
OA=OC
góc AOB=góc COD
OB=OD
=>ΔOAB=ΔOCD




a: AG\(\perp\)AB
BD\(\perp\)AB
Do đó: AG//BD
b: Ta có: \(\widehat{FEB}=\widehat{FAC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên ED//AC
c: Vì \(\widehat{CHD}=\widehat{HDG}\left(=65^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên CF//DG
d: Ta có: \(\widehat{EAC}+\widehat{BAC}=\widehat{EAB}\)
=>\(\widehat{A_2}=90^0-45^0=45^0\)
Ta có: \(\widehat{EAC}=\widehat{BAC}\left(=45^0\right)\)
mà tia AC nằm giữa hai tia AB,AE
nên AC là phân giác của góc BAE
e: Xét ΔABC vuông tại B có \(\widehat{BAC}=45^0\)
nên ΔBAC vuông cân tại B
=>\(\widehat{C_1}=\widehat{A_2}=45^0\)
f: AC//ED
=>\(\widehat{C_2}=\widehat{CHD}\)(hai góc so le trong)
=>\(\widehat{C_2}=65^0\)
Ta có: \(\widehat{C_1}+\widehat{C_2}+\widehat{C_3}=180^0\)
=>\(\widehat{C_3}=180^0-65^0-45^0=70^0\)
FE//CD
=>\(\widehat{F_1}=\widehat{C_3}\)(hai góc so le trong)
=>\(\widehat{F_1}=70^0\)
CF//GD
=>\(\widehat{G_1}=\widehat{F_1}\)
=>\(\widehat{G_1}=70^0\)