( 12 \(\dfrac{1}{3}\) - 10 \(\dfrac{1}{4}\) ) : ( 2 \(\dfrac{1}{2}\) + 1 \(\dfrac{1}{3}\) )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi M là điểm chia đoạn AB (AM > MB) và AB có độ dài bằng a.
Gọi tỉ số cần tìm là x (x > 0).
Theo đề bài: 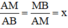
⇒ AM = x.AB = ax;
⇒ M B = x . A M = x . a x = a x 2
Ta có: MA + MB = AB
⇒ a x + a x 2 = a ⇔ x 2 + x = 1 ⇔ x 2 + x − 1 = 0
Có a = 1 ; b = 1 ; c = -1 ⇒ Δ = 1 – 4.1.(-1) = 5 > 0.
Phương trình có hai nghiệm
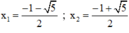
Chỉ có nghiệm 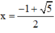 thỏa mãn điều kiện.
thỏa mãn điều kiện.
Vậy tỉ số cần tìm là: 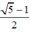
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.

hiệu khi không giảm số trừ đi 9 là:
55-9=46
hiệu ban đầu là:
46-14=32
Đ/s:32


Gọi M là điểm chia đoạn AB (AM > MB) và AB có độ dài bằng a.
Gọi tỉ số cần tìm là x (x > 0).
Theo đề bài: 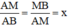
⇒ AM = x.AB = ax;
⇒MB = x.AM = x.ax = ax2
Ta có: MA + MB = AB
⇒ ax + ax2 = a
⇔ x2 + x = 1
⇔ x2 + x – 1 = 0.
Có a = 1 ; b = 1 ; c = -1 ⇒ Δ = 1 – 4.1.(-1) = 5 > 0.
Phương trình có hai nghiệm
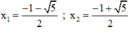
Chỉ có nghiệm 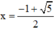 thỏa mãn điều kiện.
thỏa mãn điều kiện.
Vậy tỉ số cần tìm là: 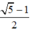

A.Lý thuyết về dấu tam thức bậc hai
1. Tam thức bậc hai (một ẩn) là đa thức có dạng f(x) = ax2 + bx + c trong đó x là biến a, b, c là các số đã cho, với a ≠ 0.
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x = , với mọi x ≠
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
2. Bất phương trình bậc hai một ẩn.
Là mệnh đề chứa một biến có một trong các dạng:
ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ax2 + bx + c ≤ 0 trong đó vế trái là một tam thức bậc hai.
Để giải bất phương trình bậc hai một ẩn ta dùng định lí về dấu của tam thức bậc hai.


Số lần so sánh giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần so sánh giữa các phần tử là cố định, không phụ thuộc vào dữ liệu đầu vào. Cụ thể, số lần so sánh trong thuật toán sắp xếp chọn là \(\dfrac{n\left(n-1\right)}{2}\), với n là số phần tử trong mảng hoặc danh sách.
Số lần hoán đổi giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần hoán đổi giữa các phần tử có thể đạt đến tối đa n-1 lần, với n là số phần tử trong mảng hoặc danh sách.
Vậy độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2), hay \(\dfrac{n\left(n-1\right)}{2}\) lần so sánh và tối đa n-1 lần hoán đổi giữa các phần tử.




\(\left(12\dfrac{1}{3}-10\dfrac{1}{4}\right):\left(2\dfrac{1}{2}+1\dfrac{1}{3}\right)\\ =\left(\dfrac{37}{3}-\dfrac{41}{4}\right):\left(\dfrac{5}{2}+\dfrac{4}{3}\right)\\ =\dfrac{25}{12}:\dfrac{23}{6}\\ =\dfrac{25}{12}\cdot\dfrac{6}{23}\\ =\dfrac{25}{46}\)