a+b+c=\(\dfrac{9}{8}\) , 0≤a,b,c≤1 tìm min P=a3+b3+c3 ; Q=\(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\) ; R=\(\dfrac{1}{1+\sqrt[3]{a}}+\dfrac{1}{1+\sqrt[3]{b}}+\dfrac{1}{1+\sqrt[3]{c}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi 60g=0,06kg, 50g=0,05kg
Lượng đường cần cho x chiếc bánh nướng là 0,06x kg
Lượng đường cần cho y chiếc bánh dẻo là 0,05y kg
Vì lượng đường đã nhập về là 500kg và lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về nên ta có:
\(0,06x + 0,05y \le 500\)

THAM KHẢO
Thuật toán:
B1. Nhập ba số dương a,b,c
B2. Nếu a+b>c và b+c>a và c+a>b thì in ra màn hình a,b,c là ba cạnh của tam giác. Ngược lại in ra a,b,c không là ba cạnh của tam giác.
B3. Kết thúc.
Chương trình:
var a,b,c: real;
begin
writeln('Nhap ba canh lan luot: '); read(a,b,c);
if (a<0) or (b<0) or (c<0) then
repeat
writeln('Khong hop le. Nhap lai ba canh lan luot: '); read(a,b,c);
until (a>0) and (b>0) and (c>0);
if (a+b>c) and (b+c>a) and (c+a>b) then writeln('Ba so nay la do dai ba canh tam giac') else writeln('Ba so nay khong la ba canh cua tam giac');
end.

Áp dụng bđt \(\frac{x^2}{m}+\frac{y^2}{n}+\frac{z^2}{p}\ge\frac{\left(x+y+z\right)^2}{m+n+p}\) ta có
\(\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{a^2+b^2+c^2}=a^2+b^2+c^2\)
Bài 1. Đặt \(a=\sqrt{x+3},b=\sqrt{x+7}\)
\(\Rightarrow a.b+6=3a+2b\) và \(b^2-a^2=4\)
Từ đó tính được a và b
Bài 2. \(\frac{2x-1}{x^2}+\frac{y-1}{y^2}+\frac{6z-9}{z^2}=\frac{9}{4}\)
\(\Leftrightarrow\frac{2}{x}-\frac{1}{x^2}+\frac{1}{y}-\frac{1}{y^2}+\frac{6}{z}-\frac{9}{z^2}-\frac{9}{4}=0\)
Đặt \(a=\frac{1}{x},b=\frac{1}{y},c=\frac{1}{z}\)
Ta có \(2a-a^2+b-b^2+6c-9c^2-\frac{9}{4}=0\)
\(\Leftrightarrow-\left(a^2-2a+1\right)-\left(b^2-b+\frac{1}{4}\right)-\left(9c^2-6c+1\right)=0\)
\(\Leftrightarrow-\left(a-1\right)^2-\left(b-\frac{1}{2}\right)^2-\left(3c-1\right)^2=0\)
Áp dụng tính chất bất đẳng thức suy ra a = 1 , b = 1/2 , c = 1/3
Rồi từ đó tìm được x,y,z

Bài 1. Từ giả thiết, với chú ý abc=1, ta suy ra \(\left(a+b\right)+c=\frac{a+b}{ab}+\frac{1}{c}=c\left(a+b\right)+\frac{1}{c}\to\left(a+b\right)\left(c-1\right)=\frac{c^2-1}{c}\to\left(c-1\right)\left(a+b-\frac{c+1}{c}\right)=0\)
\(\to\frac{\left(c-1\right)\left(ac+bc-c-1\right)}{c}=0\to\left(c-1\right)\left(\frac{1}{b}-1+c\left(b-1\right)\right)=0\to\left(c-1\right)\left(b-1\right)\left(c-\frac{1}{b}\right)=0\)
\(\to\left(c-1\right)\left(b-1\right)\left(a-1\right)=0\). Vậy ba số a,b,c có 1 số bằng 1.
Bài 2. Từ giả thiết ta suy ra\(x^3+2xy^2+\left(x^2+8y^2\right)y=0\to x^3+x^2y+2xy^2+8y^3=0\to\)
Nếu y=0 thì x=0, khi đó không thỏa mãn \(x^2+8y^2=12\) (loại).
Với y khác 0, chia cả hai vế cho \(y^3,\) ta được
\(t^3+t^2+2t+8=0\to\left(t+2\right)\left(t^2-t+4\right)=0\to t=-2\to x=-2y\)
Thế vào phương trình thứ hai ta được \(12y^2=12\to y=\pm1\to x=\mp2.\)
Vậy ta có hai cặp nghiệm \(\left(x,y\right)=\left(2,-1\right);\left(-2;1\right).\)
Bài 1. Từ giả thiết, với chú ý abc=1, ta suy ra $\left(a+b\right)+c=\frac{a+b}{ab}+\frac{1}{c}=c\left(a+b\right)+\frac{1}{c}\to\left(a+b\right)\left(c-1\right)=\frac{c^2-1}{c}\to\left(c-1\right)\left(a+b-\frac{c+1}{c}\right)=0$(a+b)+c=a+bab +1c =c(a+b)+1c →(a+b)(c−1)=c2−1c →(c−1)(a+b−c+1c )=0
$\to\frac{\left(c-1\right)\left(ac+bc-c-1\right)}{c}=0\to\left(c-1\right)\left(\frac{1}{b}-1+c\left(b-1\right)\right)=0\to\left(c-1\right)\left(b-1\right)\left(c-\frac{1}{b}\right)=0$→(c−1)(ac+bc−c−1)c =0→(c−1)(1b −1+c(b−1))=0→(c−1)(b−1)(c−1b )=0
$\to\left(c-1\right)\left(b-1\right)\left(a-1\right)=0$→(c−1)(b−1)(a−1)=0. Vậy ba số a,b,c có 1 số bằng 1.
Bài 2. Từ giả thiết ta suy ra$x^3+2xy^2+\left(x^2+8y^2\right)y=0\to x^3+x^2y+2xy^2+8y^3=0\to$x3+2xy2+(x2+8y2)y=0→x3+x2y+2xy2+8y3=0→
Nếu y=0 thì x=0, khi đó không thỏa mãn $x^2+8y^2=12$x2+8y2=12 (loại).
Với y khác 0, chia cả hai vế cho $y^3,$y3, ta được
$t^3+t^2+2t+8=0\to\left(t+2\right)\left(t^2-t+4\right)=0\to t=-2\to x=-2y$t3+t2+2t+8=0→(t+2)(t2−t+4)=0→t=−2→x=−2y
Thế vào phương trình thứ hai ta được $12y^2=12\to y=\pm1\to x=\mp2.$12y2=12→y=±1→x=∓2.
Vậy ta có hai cặp nghiệm $\left(x,y\right)=\left(2,-1\right);\left(-2;1\right).$(x,y)=(2,−1);(−2;1).
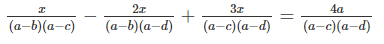
Min P em có thể tự tìm đơn giản bằng AM-GM
Min R cũng khá đơn giản:
Đặt \(\left(\sqrt[3]{a};\sqrt[3]{b};\sqrt[3]{c}\right)=\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}0\le x;y;z\le1\\x^3+y^3+z^3=\dfrac{9}{8}\end{matrix}\right.\)
\(R=\dfrac{1}{1+x}+\dfrac{1}{1+y}+\dfrac{1}{1+z}\ge\dfrac{9}{3+x+y+z}\ge\dfrac{9}{3+\sqrt[3]{9\left(x^3+y^3+z^3\right)}}=\dfrac{6}{2+\sqrt[3]{3}}\)
Xét \(Q=x+y+z\)
Do \(\left(x+y+z\right)^3\ge x^3+y^3+z^3=\dfrac{9}{8}\Rightarrow x+y+z\ge\sqrt[3]{\dfrac{9}{8}}>1\Rightarrow Q-1>0\)
\(x^3+y^3+z^3=\left(x+y+z\right)^3-3\left(x+y+z\right)\left(xy+yz+zx\right)+3xyz\)
\(\Rightarrow\dfrac{9}{8}=Q^3-3Q\left(xy+yz+zx\right)+3xyz\)
\(\Rightarrow\dfrac{9}{8}=Q^3-3\left(Q-1\right)\left(xy+yz+zx\right)-3\left(xy+yz+zx-xyz\right)\)
Do \(0\le x;y;z\le1\Rightarrow\left(1-x\right)\left(1-y\right)\left(1-z\right)\ge0\)
\(\Rightarrow xy+yz+zx-xyz\ge Q-1\) (1)
\(\Rightarrow xy+yz+zx\ge xyz+Q-1\ge Q-1\) (2)
(1);(2)\(\Rightarrow\dfrac{9}{8}\le Q^3-3\left(Q-1\right)\left(Q-1\right)-3\left(Q-1\right)\)
\(\Rightarrow8Q^3-24Q^2+24Q-9\ge0\)
\(\Rightarrow\left(2Q-3\right)\left(4Q^2-6Q+3\right)\ge0\)
Do \(4Q^2-6Q+3=4\left(Q-\dfrac{3}{4}\right)^2+\dfrac{3}{4}>0;\forall Q\)
\(\Rightarrow2Q-3\ge0\Rightarrow Q\ge\dfrac{3}{2}\)
\(Q_{min}=\dfrac{3}{2}\) khi \(\left(x;y;z\right)=\left(0;1;\dfrac{1}{2}\right)\) và hoán vị hay \(\left(a;b;c\right)=\left(0;1;\dfrac{1}{8}\right)\) và hoán vị