Giúp mình với ạ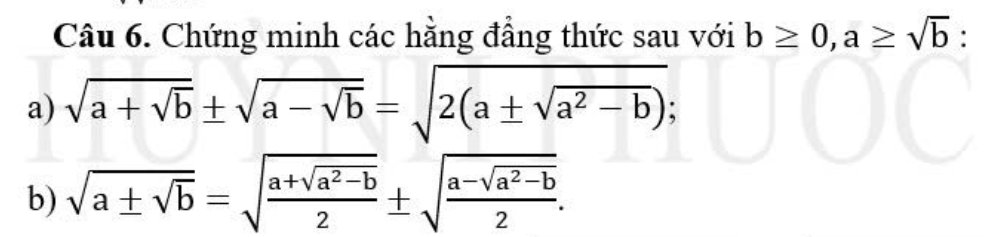
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Căn bậc hai số học của một số nguyên dương x là a sao cho
\(\left\{{}\begin{matrix}a>0\\a^2=x\end{matrix}\right.\)
Hằng đẳng thức về căn thức là:
\(\sqrt{A^2}=\left|A\right|\)
Quy tắc:
\(\sqrt{A^2\cdot B}=\sqrt{B}\cdot\left|A\right|\)
\(\sqrt{\dfrac{A}{B}}=\dfrac{\sqrt{A}}{\sqrt{B}}\)
\(\sqrt{A\cdot B}=\sqrt{A}\cdot\sqrt{B}\)

\(\sqrt{x+2\sqrt{x-1}}=2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}\right)^2+2\sqrt{x-1}+1}=2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}+1\right)^2}=2\)
\(\Leftrightarrow\left|\sqrt{x-1}+1\right|=2\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-1}+1=2\\\sqrt{x-1}+1=-2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-1}=1\Leftrightarrow x-1=1\Leftrightarrow x=2\\\sqrt{x-1}=-3\left(vl\right)\end{cases}}\)
Vậy phương trình có tập nghiệm \(S=\left\{2\right\}\)


\(\sqrt{11+4\sqrt{6}}=\sqrt{8+4\sqrt{6}+3}=\sqrt{\left(2\sqrt{2}+\sqrt{3}\right)^2}=2\sqrt{2}+\sqrt{3}\)
\(\sqrt{11+4\sqrt{6}}\)=\(\sqrt{\left(2\sqrt{2}\right)^2+2.2\sqrt{2}.\sqrt{3}+\left(\sqrt{3}\right)^3}\)=\(\sqrt{\left(2\sqrt{2}+\sqrt{3}\right)^2}\)=\(2\sqrt{2}\)+\(\sqrt{3}\)


cosα = OH¯; sinα = OK¯
Do tam giác OMK vuông tại K nên:
sin2 α + cos2 α = OK¯2 + OH¯2 = OK2 + MK2 = OM2 = 1.
Vậy sin2 α + cos2 α = 1.
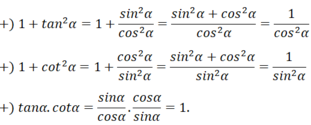


Nếu chứng minh $\sqrt{x}+\sqrt{x+1}=1$ thì không có đủ cơ sở để cm bạn nhé. Bạn viết lại đề hoặc bổ sung thêm điều kiện để mọi người trợ giúp tốt hơn.
a: Đặt \(B=\sqrt{a+\sqrt{b}}\pm\sqrt{a-\sqrt{b}}\)
\(B^2=a+\sqrt{b}+a-\sqrt{b}\pm2\sqrt{\left(a+\sqrt{b}\right)\left(a-\sqrt{b}\right)}\)
\(=2a\pm2\sqrt{a^2-b}=2\left(a\pm\sqrt{a^2-b}\right)\)
=>\(B=\sqrt{2\left(a\pm\sqrt{a^2-b}\right)}\)
b: Đặt \(A=\sqrt{\dfrac{a+\sqrt{a^2-b}}{2}}\pm\sqrt{\dfrac{a-\sqrt{a^2-b}}{2}}\)
=>\(A^2=\dfrac{a+\sqrt{a^2-b}}{2}+\dfrac{a-\sqrt{a^2-b}}{2}\pm2\sqrt{\dfrac{a^2-\left(\sqrt{a^2-b}\right)^2}{4}}\)
\(=\dfrac{2a}{2}\pm2\cdot\dfrac{\sqrt{a^2-a^2+b}}{2}\)
\(=a\pm\sqrt{b}\)
=>\(A=\sqrt{a\pm\sqrt{b}}\)