(3x-5)(2y + 7) = 100
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt ![]() ta có phương trình 6u – 8 = 3u + 7.
ta có phương trình 6u – 8 = 3u + 7.
Giải phương trình này:
6u – 8 = 3u + 7
⇔ 6u – 3u = 7 + 8
⇔ 3u = 15 ⇔ u = 5
Vậy (16x + 3)/7 = 5 ⇔ 16x + 3 = 35
⇔ 16x = 32 ⇔ x = 2
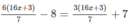
⇔ (16x + 3)/7 = 5 ⇔ 16x + 3 = 35
⇔ 16x = 32 ⇔ x = 2

1. 3x( x - 2 ) - ( x - 2 ) = 0
<=> ( x-2).(3x-1) = 0 => x = 2 hoặc x = \(\dfrac{1}{3}\)
2. x( x-1 ) ( x2 + x + 1 ) - 4( x - 1 )
<=> ( x - 1 ).( x (x^2 + x + 1 ) - 4 ) = 0
(phần này tui giải được x = 1 thôi còn bên kia giải ko ra nha )
3 \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\\sqrt{5}x-5y=10\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=-1\\x=\sqrt{5}\end{matrix}\right.\)
\(1. 3x^2 - 7x +2=0\)
=>\(Δ=(-7)^2 - 4.3.2\)
\(= 49-24 = 25\)
Vì 25>0 suy ra phương trình có 2 nghiệm phân biệt:
\(x_1\)=\(\dfrac{-\left(-7\right)+\sqrt{25}}{2.3}=\dfrac{7+5}{6}=2\)
\(x_2\)=\(\dfrac{-\left(-7\right)-\sqrt{25}}{2.3}=\dfrac{7-5}{6}=\dfrac{1}{3}\)

xy+3x-2y-7=0
=>(xy-2y)+3x-7=0
=>y(x-2)+3x-6=-1
=>y(x-2)+3(x-2)=-1
=>(y+3)(x-2)=-1
=>y+3 và x-2 thuộc Ư(1)={1;-1}
Xét y+3=1 =>y=2 <=>x-2=-1 =>x=1
Xét y+3=-1 =>y=-4 <=>x-2=1 =>x=3

nhâ vế 1 vs 2
nhân vế 2 vs 3 là ra thôi bn
trừ 2 vế cho nhau nữa
\(\left\{{}\begin{matrix}3x+2y=4\\2x-3y=7\end{matrix}\right.< =>\left\{{}\begin{matrix}6x+4y=8\\6x-9y=21\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}13y=-13\\3x+2y=4\end{matrix}\right.< =>\left\{{}\begin{matrix}y=-1\\3x=4+2=6\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}y=-1\\x=2\end{matrix}\right.\)

a) Ta có: Δ = 196 > 0
Phương trình có 2 nghiệm x 1 = 3 , x 2 = 1 5
b) Đặt t = x 2 , t ≥ 0 , phương trình trở thành t 2 + 9 t − 10 = 0
Giải ra được t=1 (nhận); t= -10 (loại)
Khi t=1, ta có x 2 = 1 ⇔ x = ± 1 .
c) 3 x − 2 y = 10 x + 3 y = 7 ⇔ 3 x − 2 y = 10 ( 1 ) 3 x + 9 y = 21 ( 2 )
(1) – (2) từng vế ta được: y=1
Thay y= 1 vào (1) ta được x= 4
Vậy hệ phương trình có nghiệm duy nhất là x= 4; y= 1.

a: =>1,5x^2-2x+1,2x-1,5x^2>=0,32
=>-0,8x>=0,32
=>x<=4
b: =>60x^2+35x-60x^2+15x<=-100
=>50x<=-100
=>x<=-2

a)\(0,5x\left(3x-4\right)+1,5x\left(0,7-x\right)\ge0,32\)
\(\Leftrightarrow1,5x^2-2+1,05-1,5x^2\ge0,32\)
\(\Leftrightarrow1,5x^2-1,5x^2-2+1,05\ge0,32\)
\(\Leftrightarrow-0,95\ge0,32\)(vô lí)
Vậy bất phương trình vô nghiệm
b)\(5x\left(12x+7\right)-3x\left(20x-5\right)\le-100\)
\(\Leftrightarrow60x^2+35x-60x^2+15x\le-100\)
\(\Leftrightarrow50x\le-100\)
\(\Leftrightarrow x\le-2\)
Vậy bất phương trình có nghiệm là \(S=\left\{xIx\le-2\right\}\)
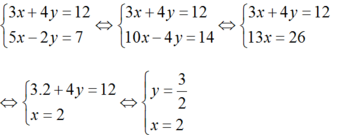
(3x-5)(2y+7)=100
=>(3x-5;2y+7)\(\in\){(1;100);(100;1);(-1;-100);(-100;-1);(2;50);(50;2);(-2;-50);(-50;-2);(4;25);(25;4);(-4;-25);(-25;-4);(5;20);(20;5);(-5;-20);(-20;-5);(10;10);(-10;-10)}
=>(3x;2y)\(\in\){(6;93);(105;-6);(4;-107);(-95;-8);(7;43);(55;-5);(3;-57);(-45;-9);(9;18);(30;-3);(1;-32);(-20;-11);(10;13);(25;-2);(0;-27);(-15;-12);(15;3);(-5;-17)}
=>(x;y)\(\in\){(2;93/2);(35;-3);(4/3;-107/2);(-95/3;-4);(7/3;43/2);(55/3;-5/2);(1;-57/2);(-15;-9/2);(3;9);(10;-3/2);(1/3;-16);(-20/3;-11/2);(10/3;13/2);(25/3;-1);(0;-27/2);(-5;-6);(5;3/2);(-5/3;-17/2)}
(3x - 5)(2y + 7) = 100
Ta có: 100 = 1 x 100 = 2 x 50 = 4 x 25
Do 2y + 7 là số lẻ nên 2y + 7 chỉ có thể = 1 hoặc 25
Trường hợp 1: 2y + 7 = 1
⇒ 2y = 1 - 7
⇒ 2y = -6
⇒ y = (-6) : 2
⇒ y = -3
Vậy 3x - 5 = 100
⇒ 3x = 100 + 5
⇒ 3x = 105
⇒ x = 105 : 3
⇒ x = 35
Trường hợp 2: 2y + 7 = 25
⇒ 2y = 25 - 7
⇒ 2y = 18
⇒ y = 18 : 2
⇒ y = 9
Vậy 3x - 5 = 4
⇒ 3x = 4 + 5
⇒ 3x = 9
⇒ x = 9 : 3
⇒ x = 3
Vậy (x; y) ϵ {(35; -3); (3; 9)}