x2(x3+1)=0
Tìm các số nguyên x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 1 2024
a: (x-1)(x+2)(-x-3)=0
=>(x-1)(x+2)(x+3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x+2=0\\x+3=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=-2\\x=-3\end{matrix}\right.\)
b: (x-7)(x+3)<0
TH1: \(\left\{{}\begin{matrix}x-7>0\\x+3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>7\\x< -3\end{matrix}\right.\)
=>\(x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-7< 0\\x+3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 7\\x>-3\end{matrix}\right.\)
=>-3<x<7
mà x nguyên
nên \(x\in\left\{-2;-1;0;1;2;3;4;5;6\right\}\)
CM
29 tháng 12 2017
Chọn A.
Với x >1 ta có hàm số f(x) = x2 liên tục trên khoảng (1; +∞). (1)
Với 0 < x < 1 ta có hàm số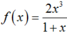 
liên tục trên khoảng (0; 1). (2)
Với x < 0 ta có f(x) = x.sinx liên tục trên khoảng (-∞; 0). (3)
Với x = 1 ta có f(1) = 1;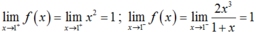 
Suy ra 
.
Vậy hàm số liên tục tại x = 1.
Với x = 0 ta có f(0) = 0;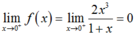 
;
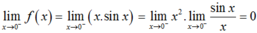suy ra 
.
Vậy hàm số liên tục tại x = 0. (4)
Từ (1), (2), (3) và (4) suy ra hàm số liên tục trên R.
Chọn A.
22 tháng 8 2021
\(x^3-0,25=0\\ \Rightarrow x^3=0,25\\ \Rightarrow x=\sqrt[3]{0,25}\)
Y
16 tháng 3 2022
var n:integer;
begin
write('Nhap n: '); readln(n);
if (n mod 3 =0) then
write(n,' chia het cho 3')
else
write(m,' k chia het cho 3');
readln;
end.
16 tháng 3 2022
#include <bits/stdc++.h>
using namespace std;
long long x,n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1;i<=n; i++)
{
cin>>x;
if (x%3==0) t+=x;
}
cout<<t;
return 0;
}
24 tháng 5 2023
=>(x1+x2)^2+x1x2=1
=>(-2m)^2+(-3)=1
=>4m^2=4
=>m=-1 hoặc m=1
KV
25 tháng 5 2023
Do a = 1 và c = -3
⇒ a và c trái dấu
⇒ Phương trình luôn có hai nghiệm phân biệt
Theo Viét, ta có:
x₁ + x₂ = -2m
x₁x₂ = -3
Lại có:
x₁² + x₂² + 3x₁x₂ = 1
⇔ x₁² + 2x₁x₂ + x₂² + x₁x₂ = 1
⇔ (x₁ + x₂)² + x₁x₂ = 1
⇔ (-2m)² - 3 = 1
⇔ 4m² = 4
⇔ m² = 1
⇔ m = -1 hoặc m = 1
Vậy m = -1; m = 1 thì phương trình đã cho có hai nghiệm phân biệt x₁, x₂ thỏa mãn: x₁² + x₂² + 3x₁x₂ = 1
1,x=0
hoặc: x = -1