Tìm các số nguyên x, y biết:
a) (x + 4) . (y - 1) = 13
b) xy - 3x + y = 20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mấy cái này dễ mà k lm đc à ......................................nói v thui chứ t cũng k bik làm ^^
a) thay m=2 ... tự thay
\(\Leftrightarrow\int^{2y+x=2\left(1\right)}_{2x-2y=1\left(2\right)}\)
=>2y+x-2=0(1)
=>-2y+2x-1=0(2)
=>-(2y-2x+1)=0(2)
=>2y-2x+1=0(2)
vẽ đồ thị hàm số ra
=>x=1;\(y=\frac{1}{2}\)hoặc 0,5
b,c ko biết nên ns thế nào ^^

a) Với m = -2
=> hpt trở thành: \(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}y=2-x\\-x=0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Vậy S = {0; 2}
b) Ta có: \(\left\{{}\begin{matrix}x+y=2\left(1\right)\\mx-y=m\left(2\right)\end{matrix}\right.\)
=> x + mx = 2 + m
<=> x(m + 1) = 2 + m
Để hpt có nghiệm duy nhất <=> \(m\ne-1\)
<=> x = \(\dfrac{m+2}{m+1}\) thay vào pt (1)
=> y = \(2-\dfrac{m+2}{m+1}=\dfrac{2m+2-m-2}{m+1}=\dfrac{m}{m+1}\)
Mà 3x - y = -10
=> \(3\cdot\dfrac{m+2}{m+1}-\dfrac{m}{m+1}=-10\)
<=> \(\dfrac{2m+6}{m+1}=-10\) <=> m + 3 = -5(m + 1)
<=> 6m = -8
<=> m = -4/3
c) Để hpt có nghiệm <=> m \(\ne\)-1
Do x;y \(\in\) Z <=> \(\left\{{}\begin{matrix}\dfrac{m+2}{m+1}\in Z\\\dfrac{m}{m+1}\in Z\end{matrix}\right.\)
Ta có: \(x=\dfrac{m+2}{m+1}=1+\dfrac{1}{m+1}\)
Để x nguyên <=> 1 \(⋮\)m + 1
<=> m +1 \(\in\)Ư(1) = {1; -1}
<=> m \(\in\) {0; -2}
Thay vào y :
với m = 0 => y = \(\dfrac{0}{0+1}=0\)(tm)
m = -2 => y = \(\dfrac{-2}{-2+1}=2\)(tm)
Vậy ....

Từ phương trình (2) ta có y = 3m – 1 – mx. Thay vào phương trình (1) ta được:
x + m ( 3 m – 1 – m x ) = m + 1 ( m 2 – 1 ) x = 3 m 2 – 2 m – 1 (3)
Hệ có nghiệm duy nhất khi và chỉ khi (3) có nghiệm duy nhất, tức là
m 2 – 1 ≠ 0 ⇔ m ≠ ± 1
Khi đó x = 3 m 2 − 2 m − 1 m 2 − 1 = m − 1 3 m + 1 m − 1 m + 1 = 3 m + 1 m + 1 y = 3 m − 1 − m . 3 m + 1 m + 1 = m − 1 m + 1
Hay x = 3 m + 1 m + 1 = 3 − 2 m + 1 y = m − 1 m + 1 = 1 − 2 m + 1
Vậy x, y nguyên khi và chỉ khi 2 m + 1 nguyên.
Do đó m + 1 chỉ có thể là −2; −1; 1; 2. Vậy m ∈ {−3; −2; 0} hoặc m = 1 (loại)
Đáp án:C

Thay \(m=-2\) vào \(mx-y=m\) \(\Leftrightarrow-2x-y=-2\)
\(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y=-4\\-2x-y=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y+2x+y=-4-\left(-2\right)\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=-2\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x+2=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=0\end{matrix}\right.\)
Vậy tập nghiệm có hệ pt : \(\left(x;y\right)=\left(0;2\right)\)

a) Với \(m=0\) ta có:
\(\left\{{}\begin{matrix}0x+4y=10-0\\x+0y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{5}{2}\end{matrix}\right.\) (nhận trường hợp này).
Với \(m\ne0\), ta có:
\(\left\{{}\begin{matrix}mx+4y=10-m\\x+my=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+4y=10-m\\-mx-m^2y=-4m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(4-m^2\right)y=10-5m\left(1\right)\\x+my=4\left(2\right)\end{matrix}\right.\)
Biện luận:
Với \(m=2\) \(\left(1\right)\Rightarrow0y=0\) (phương trình vô số nghiệm),
Với \(m=-2\Rightarrow0y=20\) (phương trình vô nghiệm).
Với \(m\ne\pm2\Rightarrow y=\dfrac{10-5m}{4-m^2}=\dfrac{5\left(2-m\right)}{\left(2-m\right)\left(2+m\right)}=\dfrac{5}{m+2}\)
Vì \(y>0\Rightarrow\dfrac{5}{m+2}>0\Leftrightarrow m+2>0\Leftrightarrow m>-2\)
Thay \(y=\dfrac{5}{m+2}\) vào (2) ta được:
\(x+\dfrac{5m}{m+2}=4\Leftrightarrow x=\dfrac{8-m}{m+2}\)
Vì x>0 \(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}8-m>0\\m+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}8-m< 0\\m+2< 0\end{matrix}\right.\end{matrix}\right.\Rightarrow-2< m< 8\)
Vì m là số nguyên và \(m\ne2\) nên \(m\in\left\{-1;0;1;3;4;5;6;7\right\}\)
Vậy \(m\in\left\{1;0;1;3;4;5;6;7\right\}\) thì hệ đã cho có nghiệm duy nhất sao cho \(x>0,y>0\).
b) Với \(m=0\) ta có nghiệm \(\left(x;y\right)=\left(4;\dfrac{5}{2}\right)\) (loại).
Với \(m=2\). Ta có hệ vô số nghiệm với nghiệm tổng quát có dạng \(\left\{{}\begin{matrix}x\in R\\y=2-\dfrac{x}{2}\end{matrix}\right.\)
Vì y là số nguyên dương nên:
\(\left\{{}\begin{matrix}x⋮2\\2-\dfrac{x}{2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮2\\x< 4\end{matrix}\right.\). Mặt khác x>0.
\(\Rightarrow x=2\Rightarrow y=1\)
Với \(m\ne\pm2\). Ta có \(y=\dfrac{5}{m+2}\).
Vì x,y là các số nguyên dương nên x,y>0. Nên:
\(m\in\left\{-1;0;1;3;4;5;6;7\right\}\) (1')
Mặt khác: \(5⋮\left(m+2\right)\)
\(\Rightarrow m+2\inƯ\left(5\right)\)
\(\Rightarrow m+2\in\left\{1;-1;5;-5\right\}\)
\(\Rightarrow m\in\left\{-1;-3;3;-7\right\}\) (2')
Từ (1') ,(2') \(\Rightarrow m\in\left\{-1;3\right\}\)
Vậy \(m\in\left\{-1;2;3\right\}\) thì hệ có nghiệm \(\left(x;y\right)\) với x,y là số nguyên dương.


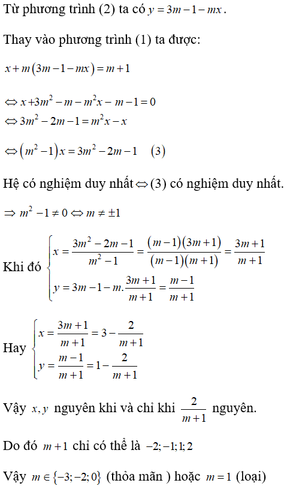
a) `(x+4)(y-1)=13`
Ta có bảng:
b) `xy-3x+y=20`
`=>(xy-3x)+(y-3)=20-3`
`=>x(y-3)+(y-3)=17`
`=>(y-3)(x+1)=17`
Ta có bảng: