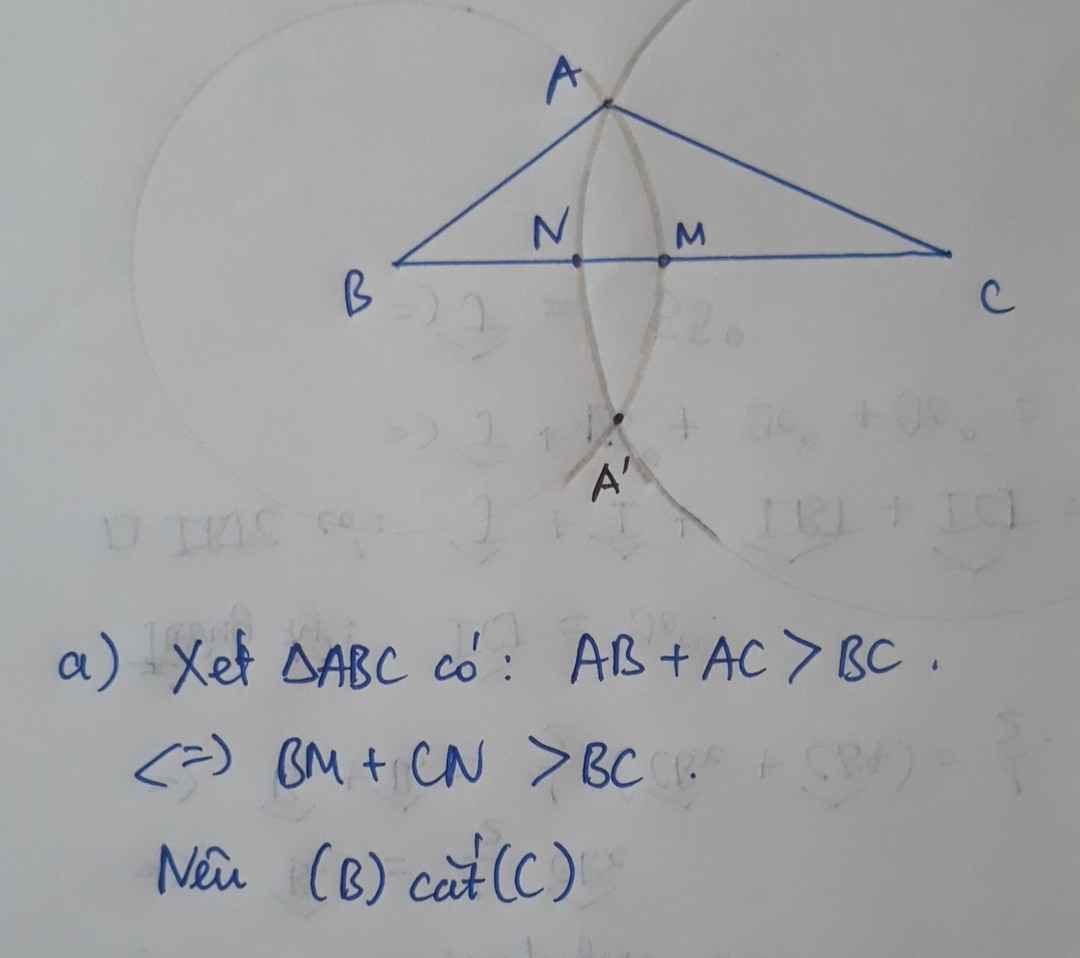
Cho tam giác ABC. a) Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A' là giao điểm khác A của hai đường tròn đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: BFEC nội tiếp
=>góc BFE+góc BCE=180 độ
=>góc AFE=góc ACB
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc AO

Bổ sung đề: đường kính BD
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
=>A nằm trên đường trung trực của BC(1)
OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC(3)
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD(4)
Từ (3) và (4) suy ra OH//DC
Xét ΔBCD có OH//DC
nên \(\dfrac{OH}{DC}=\dfrac{BO}{BD}=\dfrac{1}{2}\)
=>DC=2OH
c: Bổ sung đề; AD cắt (O) tại điểm thứ hai là E
Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔBDA vuông tại B có BElà đường cao
nên \(AE\cdot AD=AB^2\left(5\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(6\right)\)
Từ (5) và (6) suy ra \(AE\cdot AD=AH\cdot AO\)
=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{EAH}\) chung
Do đó: ΔAEH đồng dạng với ΔAOD
=>\(\widehat{AHE}=\widehat{ADO}\)

a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI ⊥⊥ MN, OK ⊥⊥ PQ.
Trong đường tròn nhỏ, ta có: MN > PQ ⇒⇒ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK ⇒⇒ AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d) OI<OK⇒OIOA<OKOAOI<OK⇒OIOA<OKOA
⇒sinˆOAI<sinˆOAK⇒ˆOAI<ˆOAK⇒ˆOAE<ˆOAH.
a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI \bot⊥ MN, OK \bot⊥ PQ.
Trong đường tròn nhỏ, ta có: MN > PQ \Rightarrow⇒ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK \Rightarrow⇒ AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d) OI < OK\Rightarrow\frac{OI}{OA}<\frac{OK}{OA}OI<OK⇒OAOI<OAOK
\Rightarrow \sin{\widehat{OAI}}< \sin{\widehat{OAK}} \Rightarrow \widehat{OAI}<\widehat{OAK} \Rightarrow \widehat{OAE}<\widehat{OAH}.⇒sinOAI<sinOAK ⇒OAI<OAK⇒OAE<OAH.

a: góc BDC=góc BNC=90 độ
=>BDNC nội tiếp đường tròn đường kính BC
Tâm là trung điểm của BC
Bán kính là BC/2
b: góc ABK=góc ACK=1/2*sđ cung AK=90 độ
BK vuông góc AB
CH vuông góc AB
=>BK//CH
CK vuông góc AC
BH vuông góc AC
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>BH=CK
c: Gọi Ax là tiếp tuyến tại A của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AND
=>Ax//DN
=>AK vuông góc DN


a, Chú ý: A M O ^ = A I O ^ = A N O ^ = 90 0
b, A M B ^ = M C B ^ = 1 2 s đ M B ⏜
=> DAMB ~ DACM (g.g)
=> Đpcm
c, AMIN nội tiếp => A M N ^ = A I N ^
BE//AM => A M N ^ = B E N ^
=> B E N ^ = A I N ^ => Tứ giác BEIN nội tiếp => B I E ^ = B N M ^
Chứng minh được: B I E ^ = B C M ^ => IE//CM
d, G là trọng tâm DMBC Þ G Î MI
Gọi K là trung điểm AO Þ MK = IK = 1 2 AO
Từ G kẻ GG'//IK (G' Î MK)
=> G G ' I K = M G M I = M G ' M K = 2 3 I K = 1 3 A O không đổi (1)
MG' = 2 3 MK => G' cố định (2). Từ (1) và (2) có G thuộc (G'; 1 3 AO)

https://diendantoanhoc.net/index.php?app=core&module=attach§ion=attach&attach_id=20602
Vào link này xem nhé
Học tốt!!!!!!!