cho tam giác đều ABC, điểm D nằm trong tam giác thỏa mãn ADC= 150 độ . Chứng minh tam giác được tạo bởi 3 đoạn thẳng có độ dài lần lượt = AD,BD,CD là tam giác vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


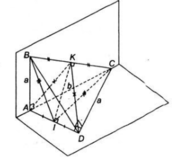


Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.

*Qua C, kẻ đường thẳng song song với AB cắt AD tại E.
- Xét △ABD có: \(AB\)//\(CE\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{BD}{CD}\) (định lí Ta-let).
Mà \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{AB}{AC}\) hay \(CE=AC\).
=>△ACE cân tại C.
=>\(\widehat{EAC}=\widehat{AEC}\).
Mà\(\widehat{AEC}=\widehat{BAD}\) ( \(AB\)//\(CE\) và so le trong).
=>\(\widehat{EAC}=\widehat{BAD}\) hay AD là phân giác của \(\widehat{BAC}\).
Xét tg ABC có
\(\dfrac{BD}{CD}=\dfrac{AB}{AC}\left(gt\right)\)
=>AD là đường phân giác

Câu hỏi của Phạm Thùy Dung - Toán lớp 7 - Học toán với OnlineMath
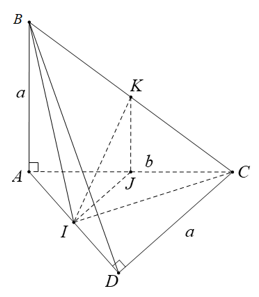


Dựng tam giác đều DAE trên mp bờ AD không chứa điểm C.
Ta thấy: ^BAD+^DAC=^BAC=600
^BAD+^EAB=^DAE=600
=> ^BAD+^DAC=^BAD+^EAB => ^DAC=^EAB
=> Tam giác ADC= Tam giác AEB (c.g.c)
=> DC=EB (2 cạnh tương ứng).
^ADC=^AEB (2 góc tương ứng)
Xét tam giác BED: ^BED=^AEB-^AED
Thay ^AEB=^ADC=1500, ^AED=600 (Do tam giác DAE đều), ta có:
^BED=1500-600=900 => ^BED vuông tại E.
Mà tam giác BED được tạo bởi 3 cạnh: EB,DE,BD
hay EB,DE,BD có độ dài thỏa mãn 3 cạnh tam giác vuông
Lại có: EB=DC (cmt), DE=AD (Tam giác DAE đều)
=> CD,AD,BD có độ dài thỏa mãn 3 cạnh trong tam giác vuông (đpcm)