Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TA CO:tam giac ABH vuong tai H(AH vuong goc BC)
=>AH^2 + BH^2=AB^2
=>AH^2+4^2=5^2
=>AH^2=9
=>Ma AH>o
NenAH=3.

a) Vì \(AB=AC\) (giả thiết)
\(\Rightarrow\Delta ABC\) cân tại A
Mà \(AM\) là đường trung tuyến (giả thiết)
\(\Rightarrow AM\) cũng là đường phân giác \(\widehat{A}\)
b) Vì \(\Delta ABC\) cân tại A (cmt)
Mà \(AM\) là đường phân giác (cmt)
\(\Rightarrow AM\) là đường trung trực \(BC\)
\(\Rightarrow AM\perp BC\)
c) Xét \(\Delta AMC\left(\widehat{M}=90^o\right)\) có:
\(AC^2=AM^2+MC^2\) (định lí pitago)
\(\Rightarrow AM=\sqrt{AC^2-MC^2}=\sqrt{5^2-\left(\dfrac{6}{2}\right)^2}=4\left(cm\right)\)
d) Xét \(\Delta AME\left(\widehat{E}=90^o\right)\) và \(\Delta AMF\left(\widehat{F}=90^o\right)\) có:
\(\widehat{EAM}=\widehat{FAM}\) (do \(AM\) là tia phân giác \(\widehat{EAF}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta AME=\Delta AMF\left(ch.gn\right)\)
\(\Rightarrow ME=MF\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta MEF\) cân tại \(M\)
a, Xét tam giác ABC có : AB = AC
Vậy tam giác ABC cân tại A
Lại có M là trung điểm BC hay AM là trung tuyến
=> AM đồng thời là đường phân giác ^A
b, Xét tam giác ABC cân tại A
AM là đường trung tuyến đồng thời là đường cao
hay AM vuông BC
c, Vì M là trung tuyến BC => BM = BC/2 = 6/2 = 3 cm
Theo định lí Pytago tam giác ABM vuông tại M
\(AM=\sqrt{AB^2-BM^2}=4cm\)
d, Xét tan giác AFM và tam giác AEM có :
^AFM = ^AEM = 900
AM _ chung
^FAM = ^EAM ( AM là phân giác )
Vậy tam giác AFM = tam giác AEM ( ch - gn )
=> FM = EM ( 2 cạnh tương ứng )
Xét tam giác MEF có FM = EM
Vậy tam giác MEF cân tại M
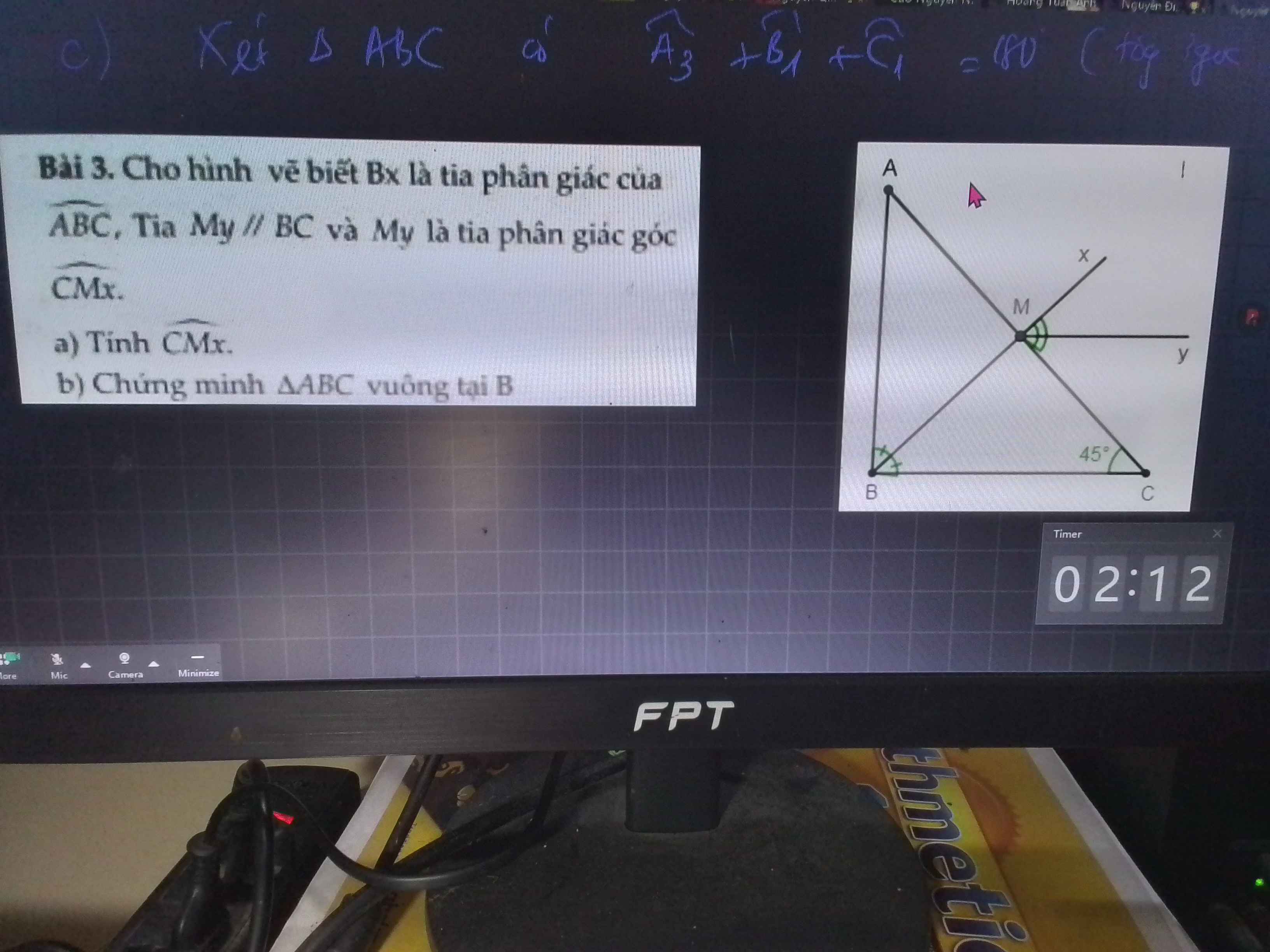
a.
Do \(My||BC\Rightarrow\widehat{CMy}=\widehat{MCB}\) (so le trong)
Mà \(\widehat{MCB}=45^0\Rightarrow\widehat{CMy}=45^0\)
lại có My là phân giác của \(\widehat{CMx}\Rightarrow\widehat{CMx}=2\widehat{CMy}\)
\(\Rightarrow\widehat{CMx}=2.45^0=90^0\)
b.
Do \(BC||My\Rightarrow\widehat{CBM}=\widehat{xMy}\)
Mà \(\widehat{xMy}=\widehat{CMy}=45^0\) (My là phân giác)
\(\Rightarrow\widehat{CBM}=45^0\)
Lại có Bx là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABC}=2\widehat{CBM}\)
\(\Rightarrow\widehat{ABC}=2.45^0=90^0\)
\(\Rightarrow\Delta ABC\) vuông tại B