tìm gtnn của :
N = x^2 +3ly-2l -1
c, k = ( x+2)^2+( y-1/5)^2 -8
các bn giải chính xác giúp mình ( mình cảm ơn nhiều nhá)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

uses crt;
var a:array[1..100]of integer;
n,i,k,max,min,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
write('Nhap k='); readln(k);
max:=a[1];
for i:=1 to n do
if max<a[i] then max:=a[i];
writeln('Gia tri lon nhat la: ',max);
writeln('Vi tri la: ');
for i:=1 to n do
if max=a[i] then write(i:4);
writeln;
min:=a[1];
for i:=1 to n do
if min>a[i] then min:=a[i];
writeln('Gia tri nho nhat la: ',min);
writeln('Vi tri la: ');
for i:=1 to n do
if min=a[i] then write(i:4);
writeln;
t:=0;
for i:=1 to n do
if i mod 2=0 then t:=t+sqr(a[i]);
writeln('Tong binh phuong cac gia tri o vi tri chan la: ',t);
readln;
end.

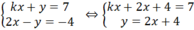
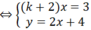
Với k + 2 ≠ 0 ⇔ k ≠ -2 thì hệ phương trình có nghiệm :
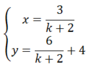
Ta có:
P = x 2 + y 2 = x 2 + 2 x + 4 2
= 5 x 2 + 16 x + 16
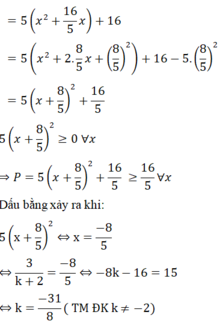
Vậy với k = (-31)/8 thì biểu thức P = x 2 + y 2 đạt giá trị nhỏ nhất

a)Ta có: \(\Delta\)= m2 - 4(m - 1) = m2 - 4m + 4 = (m - 2)2 \(\geq\)0 với mọi m
Vậy: PT có 2 nghiệm x1, x2 với mọi m
b)Theo Vi-et: x1 + x2 = m và x1x2 = m - 1
Do đó: A = x12 + x22 - 6x1x2 = (x1 + x2)2 - 8x1x2 = m2 - 8(m - 1) = m2 - 8m + 8 = ( m2 - 8m + 16) - 8 = (m - 4)2 - 8 \(\geq\)- 8 với mọi m
đúng nhé
Vậy: GTNN của A là -8 <=> m = 4

a: Khi m=2 thì pt sẽ là x^2-6x-3=0
=>\(x=3\pm2\sqrt{3}\)
`N = x^2 +3|y-2| -1`
Ta có: `{(x^2 >= 0 ),(|y-2| >=0):}`
`=> {(x^2 >= 0 ),(3|y-2| >=0):}`
`=> x^2 +3|y-2| >= 0`
`=> x^2 +3|y-2| -1 >=- 1`
Hay `N >= -1`
Dấu = xảy ra khi:
`{(x^2 = 0 ),(|y-2| =0):}`
`<=> {(x = 0 ),(y-2 =0):}`
`<=> {(x = 0 ),(y=2):}`
Vậy `N_(min) = -1 <=> {(x = 0 ),(y=2):}`
-------------------------------------------------
`K = ( x+2)^2+( y-1/5)^2 -8`
Ta có: `{(( x+2)^2 >=0),(( y-1/5)^2 >=0):}`
`=> ( x+2)^2+( y-1/5)^2 >= 0`
`=> ( x+2)^2+( y-1/5)^2 -8 >=- 8`
Hay `K >= -8`
Dấu = xảy ra khi:
`{(( x+2)^2 =0),(( y-1/5)^2 =0):}`
`<=> {( x+2 =0),( y-1/5 =0):}`
`<=> {( x=-2),( y=1/5):}`
Vậy `K_(min) = -8 <=> {( x=-2),( y=1/5):}`