Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
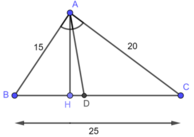
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)
a:
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot15\cdot20=150\left(cm^2\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}\)
=>\(\dfrac{BD}{CD}=\dfrac{3}{4}\)
=>\(\dfrac{CD}{BD}=\dfrac{4}{3}\)
=>\(\dfrac{CD+BD}{BD}=\dfrac{4+3}{3}\)
=>\(\dfrac{BC}{BD}=\dfrac{7}{3}\)
=>\(BD=\dfrac{3}{7}BC\)
=>\(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}\)
b: Vì I là trung điểm của BC
nên \(S_{ABI}=\dfrac{1}{2}\cdot S_{ABC}\)
=>\(\dfrac{S_{ABD}}{S_{ABI}}=\dfrac{3}{7}:\dfrac{1}{2}=\dfrac{6}{7}\)
c: \(S_{ABD}=\dfrac{3}{7}\cdot S_{ABC}=\dfrac{3}{7}\cdot140=60\left(cm^2\right)\)
\(S_{ABI}=\dfrac{7}{6}\cdot S_{ABD}=\dfrac{7}{6}\cdot60=70\left(cm^2\right)\)
ta có: \(S_{ABD}+S_{AID}=S_{ABI}\)
=>\(S_{AID}+60=70\)
=>\(S_{AID}=10\left(cm^2\right)\)
a) suýt làm được
b)mém làm xong
c)đang suy nghĩ
suy ra không làm được!thông cảm nhé!
BH = 1/3 BC => CH = 2/3BC
=> BH = 1/2CH
\(\hept{\begin{cases}S_{ABH}=\frac{BH\cdot AH}{2}\\S_{ACH}=\frac{CH\cdot AH}{2}\end{cases}}\Rightarrow S_{ABH}=\frac{1}{2}S_{ACH}=12cm^2\)
\(\Rightarrow S_{ABC}=6+12=18cm^2\)
a, Vì AD là phân giác nên \(\frac{AB}{AC}=\frac{DB}{DC}\Rightarrow\frac{DC}{AC}=\frac{DB}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\frac{DC}{AC}=\frac{DB}{AB}=\frac{BC}{AB+AC}=\frac{10}{15}=\frac{2}{3}\Rightarrow DC=6cm;DB=4cm\)
a/ Theo tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy ta có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{m}{n}\)
Hai tam giác ABD và tam giác ACD có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{BD}{CD}=\frac{m}{n}\)
b/ Ta có
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{m}{n}\Rightarrow\frac{S_{\Delta ABD}}{m}=\frac{S_{\Delta ACD}}{n}=\frac{S_{\Delta ABD}+S_{\Delta ACD}}{m+n}=\frac{S_{\Delta ABC}}{m+n}=\frac{s}{m+n}\)
\(\Rightarrow S_{\Delta ABD}=\frac{sm}{m+n}\)
Xét hai tam giác ABM và tam giác ABC có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{S_{\Delta ABC}}{2}=\frac{s}{2}\)
Mà \(S_{\Delta ADM}=S_{\Delta ABM}-S_{\Delta ABD}=\frac{s}{2}-\frac{sm}{m+n}\)
