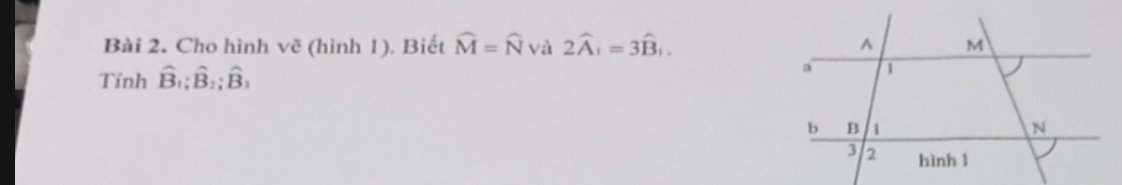
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
A P M N Q 33 o
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).

pn ơi mk hok sách giáo khoa mới cho nên bn gửi tin cho mk mk giải giúp cho
Các cặp góc đối đỉnh là
(1) Góc yOx đối đỉnh với zOt; góc zOy đối đỉnh với tOx
(2) Vì xOy kề bù với yOz
=> xOy+yOz=180 độ
=>yOz=180-xOy=180-50=130 độ
Vì zOt đối đỉnh với xOy
=> zOt=xOy=50 độ
Vậy yOz=130 độ; zOt=50 độ

x n y m t t'
Có góc xOm và góc yOn đối đỉnh
Tia Ot,Ot' lần lượt là tia phân giác của góc xOm, góc yOn.
Chứng minh tia Ot và tia Ot' là 2 tia đối nhau
Tia Ot là tia phân giác của góc xOm => góc xOt = góc tOm
Tia Ot' là tia phân giác của góc yOn => góc yOt' = góc nOt'
Mà góc xOt = góc yOn nên góc mOt = góc nOt'
=> góc mOt + góc tOn = góc mOn = 1800
=> góc tOn + góc nOt' = 1800
=> góc tOt' = 1800
Nên tia Ot và tia Ot' là 2 tia đối nhau

a)Do 5 đường cắt nhau thành 1 điểm thành 10 tia chung góc
Mà 9 tia tạo thành 9 góc
ta có tổng 10 tia nên có số góc là:
9*10=90 góc
Vì mỗi tia đều lặp lại 2 lần nên ta có số góc là:
90:2=45
b) Do 5 đường thẳng cắt nhau tại 1 điểm nên tạo được 5 góc bẹt.
=> có tất cả số khác góc bẹt là: 45-5=40(góc)
Ta có 40 góc khác góc bẹt mà 1 góc là đối đỉnh với nó => số góc đối đỉnh là là: 40:2=20 góc
c) Ta có 5 đường thẳng mà 10 góc ko có điểm nào chung
=> tổng của 10 góc này = 360o
Giả sử cả 10 góc đó < 36o
Mà nếu cả 10 góc đó <36o thì điều này sẽ ko có lý do để cho rằng là đúng
=> Trong tất cả 10 góc đó phải tồn tại 1 góc <36o (đpcm)
Cảm ơn bạn Dante Koryu nha ko ngờ bạn lại hỏi câu mà mình đang muốn hỏi.
Trùng hợp thật.!!!
 giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
Ta có: \(\widehat{M}=\widehat{N}\)
=>AM//BN
Ta có: AM//BN
=>\(\widehat{A_1}+\widehat{B_1}=180^0\)
mà \(2\widehat{A_1}=3\cdot\widehat{B_1}\)
nên \(\widehat{B_1}=180^0\cdot\dfrac{2}{5}=72^0\)
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\)(hai góc kề bù)
=>\(\widehat{B_2}+72^0=180^0\)
=>\(\widehat{B_2}=108^0\)
\(\widehat{B_3}=\widehat{B_1}\)(hai góc đối đỉnh)
mà \(\widehat{B_1}=72^0\)
nên \(\widehat{B_3}=72^0\)