giúp em với,có tick ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 8 2023
Ta có: \(\widehat{HAF}+\widehat{FAB}+\widehat{DAB}+\widehat{DAH}=360^o\)
Mà \(\widehat{FAB}=\widehat{DAH}=90^O\)
\(\Rightarrow\widehat{HAF}+\widehat{DAB}=180^o\)
Ta lại có: \(\widehat{ADC}+\widehat{DAB}=180^o\) ( 2 góc trong cùng phía nên kề bù với nhau )
\(\Rightarrow\widehat{HAF}=\widehat{ADC}\)
Xét \(\Delta HAF\) và \(\Delta ADC\) có:
\(HA=HD\left(gt\right)\)
\(\widehat{HAF}=\widehat{ADC}\left(CMT\right)\)
\(AF=DC\left(gt\right)\)
Vậy \(\Delta HAF\) \(=\) \(\Delta ADC\) \(\left(c.g.c\right)\)
\(\Rightarrow AC=FH\) ( 2 cạnh tưng ứng )
b) Ta có: \(\widehat{CBE}=\widehat{ABC}+90^o\)
\(\widehat{GDC}=\widehat{ADC}+90^o\)
Mà \(\widehat{ADC}=\widehat{ABC}\)
\(\Rightarrow\widehat{CBE}=\widehat{GDC}\)
Xét \(\Delta CBE\) và \(\Delta GDC\) ta có:
\(EB=CD\left(gt\right)\)
\(\widehat{CBE}=\widehat{GDC}\left(CMT\right)\)
\(CB=GD\left(gt\right)\)
Vậy \(\Delta CBE=\Delta GDC\left(c.g.c\right)\)
\(\Rightarrow CE=GC\) ( 2 cạnh tương ứng )
\(\Rightarrow\Delta CEG\) cân tại \(G\)
31 tháng 8 2023
a) Ta biết rằng trong hình bình hành ABCD, các đường chéo chia nhau đều và cắt nhau ở trung điểm.
Vì vậy, ta có AC = FH.
b) Vì ABFE là hình vuông, nên các cạnh AB và FE là song song và bằng nhau.
Tương tự, vì ADGH là hình vuông, nên các cạnh AD và GH cũng là song song và bằng nhau. Do đó, ta có AB || FE và AD || GH. Vì AC = FH (chứng minh ở câu a), và AB || FE, AD || GH,
nên theo tính chất của các đường song song, ta có AC || FH. Do đó, AC vuông góc với FH.
c) Ta biết rằng trong hình vuông, các đường chéo chia nhau đều và cắt nhau vuông góc.
Vì vậy, ta có AG ⊥ CE và CG ⊥ AE. Vì AG ⊥ CE, nên AGC là tam giác vuông tại G.
Vì CG ⊥ AE, nên CEG là tam giác vuông tại C. Vì AG = GC (vì AGC là tam giác vuông cân), nên ta cũng có CG = GC.
Do đó, ta có CEG là tam giác vuông cân.
Vậy, ta đã chứng minh được a), b), c) trong đề bài.
2 tháng 8 2016
nối BD và AC
trong tam giác ABC ta có: M và N lần luợt là trung đỉêm của AB và AC
=> MN là đuờng trung bình của tam giác ABC
=> MN//AC(
trong tam giác ADC ta có I và K lần luợt là trung điểm của DC và DA
=> KI là đuờng trung bình của tam giác ADC
=> KI//AC
ta có: KI//AC
MN//AC
=> KI//MN(1)
trong tam giác ABD có M và K lần luợt là trung điểm của AB và AD
=> MK là đuờng trung bình của tam giác ADB
=> MK//DB
trong tam giác CDB có I và N lần luợt là trung điểm của DC và CB
=> IN là đuờng trung bình của tam, giác CDB
=>IN//BD
ta có: MK//DB
IN//DB
=> MK//IN(2)
từ (1)(2)=> MK//IN
MN//KI
=> MNIK là hình bình hành
2 tháng 8 2016
Bài 1:Vẽ đường chéo BD
Xét tam giác ADB có:
M là trung điểm của AB
K là trung điểm của AD
=>KM là đường trung bình của tam giác ADB
=>KM//DB(1) và KM=1/2 DB(3)
Xét tam giác BCD có:
N là trung điểm của BC
I là trung điểm của DC
=>NI là đường trung bình của tam giác BCD
=>NI//DB(2) và NI=1/2DB(4)
Từ (1) và (2)=>KM//NI( //DB)(5)
Từ (3) và (4)=>KM=NI(=1/2 DB)(6)
Từ (5) và (6)=>KMNI là hình bình hành (dhnb3)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1
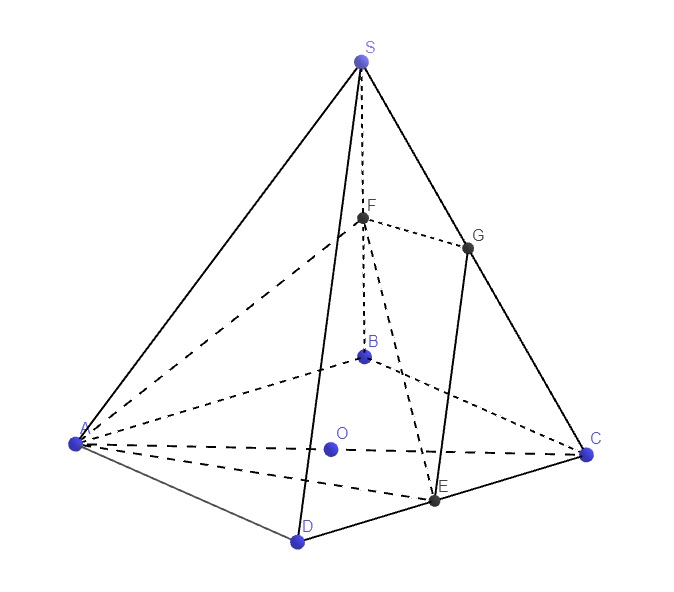
Qua E kẻ đường thẳng song song SD cắt SC tại G \(\Rightarrow\dfrac{GC}{GS}=\dfrac{EC}{ED}\) (Talet)
Mặt khác theo định lý phân giác: \(\dfrac{EC}{ED}=\dfrac{AC}{AD}\Rightarrow\dfrac{GC}{GS}=\dfrac{AC}{AD}=\dfrac{AB}{SA}\) (do AC=AB và AD=SA)
Theo định lý phân giác: \(\dfrac{AB}{SA}=\dfrac{FB}{FS}\Rightarrow\dfrac{GC}{GS}=\dfrac{FB}{FS}\Rightarrow FG||BC\Rightarrow FG||AD\)
\(\Rightarrow\left(EFG\right)||\left(SAD\right)\Rightarrow EF||SAD\)
a: Xét tứ giác BHCK có
M là trung điểm chung của BC và HK
=>BHCK là hình bình hành
b: BHCK là hình bình hành
=>BH//CK và BK//CH
Ta có: BH//CK
BH\(\perp\)AC
DO đó: CK\(\perp\)AC
Ta có:BK//CH
CH\(\perp\)AB
Do đó: BK\(\perp\)BA
c: ΔBEC vuông tại E
mà EM là đường trung tuyến
nên \(EM=\dfrac{BC}{2}\left(1\right)\)
Ta có: ΔBFC vuông tại F
mà FM là đường trung tuyến
nên \(FM=\dfrac{BC}{2}\left(2\right)\)
Từ (1),(2) suy ra ME=MF
=>ΔMEF cân tại M