tính giá trị lớn nhất hoặc nhỏ nhất nếu có 1.A=x^2-12x+11
10.M=-4x^2+12x-7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

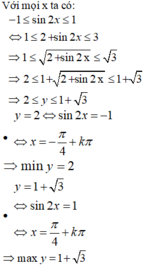
Do đó, tổng giá trị lớn nhất và nhỏ nhất của hàm số là:
![]()
Đáp án C

+ Ta có:
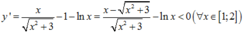
vì x < x 2 + 3 nên
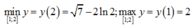
Mà trên đoạn [1 ; 2] thì 0 ≤ ln x ≤ ln 2
=> y’ < 0 ; do đó hàm số đã cho nghịch biến trên đoạn [1, 2].
+ Hàm số đã cho liên tục và xác định trên đoạn [1 ;2]
Khi đó
Do đó
![]()
Chọn D

Chọn A.
TXĐ: D = R.
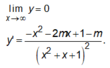
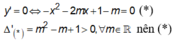 có 2 nghiệm phân biệt
có 2 nghiệm phân biệt ![]()
BBT:
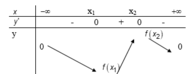
Vậy hàm số đạt giá trị lớn nhất là
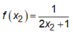
![]()
YCBT 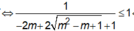
![]()
![]()
![]()
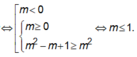

y’ = 2x ≤ 0 trên đoạn [-3; 0]. Vậy hàm số nghịch biến trên đoạn [-3,0].
Khi đó trên đoạn [-3,0]: hàm số đạt giá trị lớn nhất tại x = -3 và giá trị lớn nhất bằng 9, hàm số đạt giá trị nhỏ nhất tại x = 0 và giá trị nhỏ nhất = 0.

Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y' = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3:


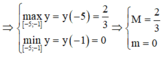
![]()
\(1,A=x^2-12x+11\\ =\left(x^2-12x+36\right)-25\\ =\left(x-6\right)^2-25\)
Ta có: `(x-6)^2>=0` với mọi x
`=>(x-6)^2-25>=-25` với mọi x
Dấu "=" xảy ra: `x-6=0<=>x=6`
\(2,M=-4x^2+12x-7\\ =\left(-4x^2+12x-9\right)+2\\ =-\left(4x^2-12x+9\right)+2\\ =-\left(2x-3\right)^2+2\)
Ta có: `(2x-3)^2>=0` với mọi x
`=>-(2x-3)^2<=0` với mọi x
`=>-(2x-3)^2+2<=2` với mọi x
Dấu "=" xảy ra: `2x-3=0<=>x=3/2`
1: \(A=x^2-12x+11\)
\(=x^2-12x+36-25\)
\(=\left(x-6\right)^2-25>=-25\forall x\)
Dấu '=' xảy ra khi x-6=0
=>x=6
10: \(M=-4x^2+12x-7\)
\(=-4x^2+12x-9+2\)
\(=-\left(2x-3\right)^2+2< =2\forall x\)
Dấu '=' xảy ra khi 2x-3=0
=>2x=3
=>\(x=\dfrac{3}{2}\)