Cho a,b,c là 3 cạnh của tam giác.CMR: √2(a+b+c) <= √a^2+b^2+√b^2+c^2+√c^2+a^2 < √3(a+b+c)
Cần gấp với ạ!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.
Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB
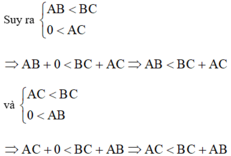
⇒ Đpcm

Với ΔDEF ta có các bất đẳng thức và quan hệ giữa các cạnh là:
DE < EF + DF
DF < EF + DE
EF < DE + DF
DF - EF < DE < DF + EF (với DF > EF)

Gọi độ dài cạnh còn lại của tam giác là c.
Áp dụng bất đẳng thức tam giác, ta có:
a – b < c < a + b
\( \Leftrightarrow \)a – b + a + b < c + a + b < a + b + a + b
\( \Leftrightarrow \)2a < chu vi tam giác < 2 (a+b)
Vậy chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a+b).

Với ∆DEF ta có các bất đẳng thức và quan hệ giữa các cạnh là:
DE < EF + DF
DF < EF + DE
EF < DE + DF
DF - EF < DE < DF + EF (với DF > EF)
Trả lời
Với ∆DEF ta có các bất đẳng thức và quan hệ giữa các cạnh là:
DE < EF + DF
DF < EF + DE
EF < DE + DF
DF - EF < DE < DF + EF (với DF > EF)

Theo kết quả câu a và câu b
MA + MB < IB + IA < CA + CB nên MA + MB < CA + CB.

a) Xét tam giác vuông AHC có AC là cạnh lớn nhất ( cạnh lớn nhất trong tam giác vuông) => AC>HC (1) Xét tam giác vuông AHB có AB là cạnh lớn nhất (canh lớn nhất trong tam giác vuông) =>AB>HB (2) Ta có : HC+HB+BC ( H nằm giũa A và C) (3) Từ (1) , (2) và (3) => AC+AB>BC b)Xét tam giác ABC có BC là cạnh lớn nhất(gt) =>BC>AB Ta có : AC>0 => BC+AC>AB Xét tam giác ABC có BC là cạnh lớn nhất (gt) =>BC>AC Vì AB>0=>BC+AB>AC

DE+DF>EF>GTTĐỐI DE-DF
DE+EF>DF>GTTĐỐI DE-EF
DF+EF>DE>GTTĐỐI DF-EF

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
Với mọi x;y dương ta có:
\(\left(x-y\right)^2\ge0\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge x^2+y^2+2xy\)
\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow\sqrt{x^2+y^2}\ge\dfrac{x+y}{\sqrt{2}}\)
Áp dụng:
\(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\ge\dfrac{a+b}{\sqrt{2}}+\dfrac{b+c}{\sqrt{2}}+\dfrac{c+a}{\sqrt{2}}=\sqrt{2}\left(a+b+c\right)\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
- Với BĐT bên phải: \(\sqrt{3}\left(a+b+c\right)>\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\)
Áp dụng BĐT Bunhiacopxki:
\(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\le\sqrt{3\left(a^2+b^2+b^2+c^2+c^2+a^2\right)}\)
\(\Leftrightarrow\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\le\sqrt{6\left(a^2+b^2+c^2\right)}\)
Nên ta chỉ cần chứng minh:
\(\sqrt{3}\left(a+b+c\right)>\sqrt{6\left(a^2+b^2+c^2\right)}\)
\(\Leftrightarrow\left(a+b+c\right)^2>2\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\)
Thật vậy, do a, b, c là 3 cạnh của 1 tam giác nên theo BĐT tam giác:
\(\left\{{}\begin{matrix}a< b+c\\b< c+a\\c< a+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2< a\left(b+c\right)\\b^2< b\left(c+a\right)\\c^2< c\left(a+b\right)\end{matrix}\right.\)
Cộng vế:
\(a^2+b^2+c^2< 2ab+2bc+2ca\) (đpcm)