so sánh 99100:11 và 9899 + 9799 + 9699 + 9599 + 9499 + 9399 + 9299 + 9199
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do A = 98 99 + 1 98 89 + 1 > 1 nên A = 98 99 + 1 98 89 + 1 > 98 99 + 1 + 97 98 89 + 1 + 97 = 98 98 98 + 1 98 98 88 + 1 = 98 98 + 1 98 88 + 1 = B
Vậy A > B

a ) X é t 1 − 25 26 = 1 26 ; 1 − 50 51 = 1 51 . V ì 1 26 > 1 51 = > 25 26 < 50 51
b ) X é t 1 − 213 321 = 108 321 ; 1 − 105 213 = 108 213 . V ì 108 321 < 108 213 = > 213 321 > 105 213
c ) X é t 1 + − 99 100 = 1 100 ; 1 + − 21 22 = 1 22 . V ì 1 100 < 1 11 = > − 99 100 > − 21 22 d ) X é t 1 + − 124 129 = 5 129 ; 1 + − 132 137 = 5 137 . V ì 5 129 > 5 137 = > − 124 129 > − 132 137

B = 1 2 ! + 2 3 ! + 3 4 ! + ... + 99 100 ! B = 2 − 1 2 ! + 3 − 1 3 ! + 4 − 1 4 ! + ... + 100 − 1 100 ! B = 2 2 ! − 1 2 ! + 3 3 ! − 1 3 ! + 4 4 ! − 1 4 ! + ... + 100 100 ! − 1 100 ! B = 1 1 ! − 1 2 ! + 1 2 ! − 1 3 ! + 1 3 ! − 1 4 ! + ... + 1 99 ! − 1 100 ! B = 1 − 1 100 ! < 1
Vậy B<1

a) Do A = 98 99 + 1 98 89 + 1 > 1 nên
A = 98 99 + 1 98 89 + 1 > 98 99 + 1 + 97 98 89 + 1 + 97 = 98 ( 98 98 + 1 ) 98 ( 98 88 + 1 ) = 98 98 + 1 98 88 + 1 = B
Vậy A > B
b) Do C = 100 2008 + 1 100 2018 + 1 < 1 nên
C= 100 2008 + 1 100 2018 + 1 > 100 2008 + 1 + 99 100 2018 + 1 + 99 = 100 ( 100 2007 + 1 ) 100 ( 100 2017 + 1 ) = 100 2007 + 1 100 2017 + 1 = D
Vậy C > D.

1) a)
Từ 1 đến 9 có : ( 9 - 1 ) : 1 + 1 = 9 ( chữ số)
Từ 10 đến 99 có : ( 99 - 10) : 1 + 1 x 2 = 180 (chữ số)
100 có 3 chữ số nên :
=> Từ 1 đến 100 có : 180 + 9+ 3 =192 (chữ số)
b) Từ 11 đến 99 có : (99 -11) : 1 + 1 x 2 = 178 (chữ số)
Mình ko chắc nữa vì giới hạn của bạn là 99 :V

1 )
Số số có một chữ số :
( 9 - 1 ) : 1 + 1 = 9 ( số )
Số chữ số để viết các số có một chữ số :
9 . 1 = 9 ( chữ số )
Số số có hai chữ số :
( 99 - 10 ) : 1 + 1 = 90 ( số )
Số chữ số để viết các số có hai chữ số :
90 . 2 = 180 ( chữ số )
Số số có 3 chữ số :
( 100 - 100 ) : 1 + 1 = 1
Số chữ số để viết các số có 3 chữ số :
3 . 1 = 3 ( chữ số )
Số chữ số dùng để viết x :
9 + 180 + 3 = 192 ( chữ số )
đ/s : ...

D=\(1-\frac{1}{2}+1-\frac{1}{6}+1-\frac{1}{12}+........+1-\frac{1}{9900}\)
\(=1-\frac{1}{1.2}+1-\frac{1}{2.3}+........+1-\frac{1}{99.100}\)
\(=99-\left(\frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{99.100}\right)\)
\(=99-\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+.....+\frac{1}{99}-\frac{1}{100}\right)\)
\(=99-\left(1-\frac{1}{100}\right)=98+\frac{1}{100}=\frac{9801}{100}\)
d=1/1.2+5/2.3+11/3.4+...+9899/99.100
=>d=1-1/2+1/2-1/3+...+1/99-1/100
=>d=1-1/100
=>d=99/100
Vậy d=99/100
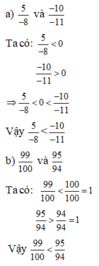
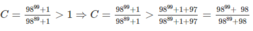
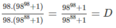
\(99^{100}:11=99.99^{99}:11=9^{99}.\left(99:11\right)=9.9^{99}\).
Vì vậy:
\(99^{100}:11=9.99^{99}=99^{99}+99^{99}+99^{99}+99^{99}+99^{99}+99^{99}+99^{99}+99^{99}+99^{99}\)\(>98^{99}+97^{99}+96^{99}+95^{99}+94^{99}+93^{99}+92^{99}+91^{11}\).
thank you