Một đề thi trắc nghiệm có 50 câu, mỗi câu có 4 đáp án và chỉ có 1 đáp án đúng. Một thí sinh lam bai thi có 2 câu thí sinh đó chọn ngẫu nhiên 1 đâp án. xác suất để cat 2 câu đó đều đúng là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố học sinh chỉ chọn đúng đáp án của 25 câu hỏi
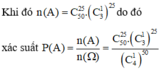

Xác suất bạn đó đúng cả 50 câu là \(\left(\dfrac{1}{4}\right)^{50}\), sai cả 50 câu là \(\left(\dfrac{3}{4}\right)^{50}\)
Giả sử bạn học sinh chọn được x câu đúng với \(0< x< 50\), trong 1 câu hỏi thì xác suất chọn được đáp án đúng là \(\dfrac{1}{4}\) và đáp án sai là \(\dfrac{3}{4}\)
Do đó xác suất để bạn đó đạt được x câu đúng là:
\(P\left(x\right)=C_{50}^x.\left(\dfrac{1}{4}\right)^x.\left(\dfrac{3}{4}\right)^{50-x}\)
\(\left\{{}\begin{matrix}P\left(x\right)\ge P\left(x-1\right)\\P\left(x\right)\ge P\left(x+1\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}C_{50}^x\left(\dfrac{1}{4}\right)^x\left(\dfrac{3}{4}\right)^{50-x}\ge C_{50}^{x-1}\left(\dfrac{1}{4}\right)^{x-1}\left(\dfrac{3}{4}\right)^{51-x}\\C_{50}^x\left(\dfrac{1}{4}\right)^x\left(\dfrac{3}{4}\right)^{50-x}\ge C_{50}^{x+1}\left(\dfrac{1}{4}\right)^{x+1}\left(\dfrac{3}{4}\right)^{49-x}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{51-x}{4x}\ge\dfrac{3}{4}\\\dfrac{x+1}{50-x}.\dfrac{3}{4}\ge\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\dfrac{47}{4}\le x\le\dfrac{51}{4}\Rightarrow x=12\)
Hay học sinh đó dễ đạt được \(2,4\) điểm nhất

Chọn đáp án B
Gọi x là số câu bạn An chọn đúng thì 50 - x là số câu mà bạn An chọn sai.
Khi đó số điểm mà bạn An đạt được là
![]()
Để bạn An làm được 4 điểm thì x = 30
Do đó bạn An chọn đúng 30 câu và chọn sai 20 câu.
Do bạn An chọn ngẫu nhiên cả 50 câu hỏi, mỗi câu có 4 phương án trả lời nên số khả năng mà bạn An chọn đáp án là 4 50
Suy ra số phần tử của không gian mẫu là 4 50
Gọi X là biến cố "Bạn Hoa chọn đúng 30 câu và chọn sai 20 câu". Vì mỗi câu chỉ có 1 phương án trả lời đúng và 3 phương án còn lại sai nên số khả năng thuận lợi cho biến cố X là C 50 30 . 3 20 Suy ra n X = C 50 30 . 3 20
Vậy xác suất cần tính là
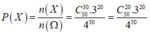

Đáp án B
Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng nhiều hơn 2 trong 5 câu còn lại. Xác suất mỗi câu chọn đúng là 1 4 và không chọn đúng là 3 4 .
Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng hoặc 3 hoặc 4 hoặc 5 trong 5 câu còn lại.
Do đó xác suất cần tìm là ![]()

Đáp án D
Để được 6 điểm học sinh đó cần trả lời đúng 30 câu.
Khi đó xác suất sẽ bằng 0 , 25 30 . 0 , 75 20 . C 50 20 .

Đáp án A
Mỗi câu trả lời đúng được 0,2 điểm => để đạt được 6 điểm, thí sinh đó phải trả lời đúng 6 0 , 2 = 30 câu
Xác suất trả lời đúng một câu là 1 4 = 0 , 25 xác suất trả lời sai một câu là 3 4 = 0 , 75
Có C 50 30 cách trả lời đúng 30 trong 50 câu, 20 câu còn lại đương nhiên trả lời sai.
Vậy xác suất để thí sinh đó đạt 6 điểm sẽ là:
![]()

Đáp án D
Để được 6 điểm học sinh đó cần trả lời đúng 30 câu.
Khi đó xác suất sẽ bằng C 50 30 0 , 25 30 0 , 75 20 .

Đáp án A.
Phương pháp: Tính xác suất để học sinh đúng thêm 3 câu nữa trở lên.
Xác suất mỗi câu trả lời đúng là 0,25 và mỗi câu trả lời sai là 0,75.
Cách giải:
An trả lời chắc chắn đúng 45 câu nên có chắc chắn 9 điểm.
Để điểm thi ≥ 9,5 => An phải trả lời đúng từ 3 câu trở lên nữa.
Xác suất để trả lời đúng 1 câu hỏi là 0,25 và trả lời sai là 0,75
TH1: Đúng 3 câu. P1 = 0,253.0,752
TH2: Đúng 49 câu P2 = 0,254.0,75
TH3: Đúng cả 50 câu P3 = 0,254
Vậy xác suất để An được trên 9,5 điểm là P = P1 + P2 + P3 = 13/1024.


Xác suất đúng của mỗi đáp án là: \(\dfrac{1}{4}\)
Xác suất cả 2 câu đều đúng là: \(\dfrac{1}{4}.\dfrac{1}{4}=\dfrac{1}{16}\)