Câu 1: Cho tam giác ABC nhọn và các đường cao AD, BE, CF. Gọi M, N lần
lượt là hình chiếu của D trên AB và AC. Chứng minh:
a) 𝐴𝐵. 𝐴𝐹 = 𝐴𝐶. 𝐴𝐸
b) 𝐴𝑁. 𝐴𝐹 = 𝐴𝑀. 𝐴𝐸
c) 𝑀𝑁//𝐸𝐹
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
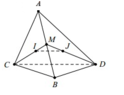
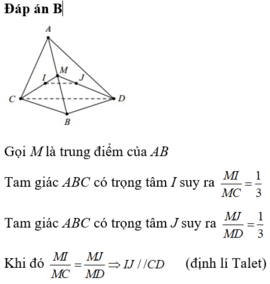
Gọi M là trung điểm của AB
Tam giác ABC có trọng tâm I suy ra M I M C = 1 3
Tam giác ABC có trọng tâm J suy ra M J M D = 1 3
Khi đó M I M C = M J M D ⇒ I J / / C D (định lí Talet)

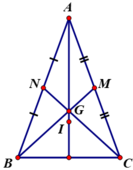
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà 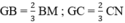 (Tính chất trọng tâm của tam giác)
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
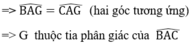
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của 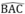
Vì G, I cùng thuộc tia phân giác của 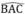 nên A, G, I thẳng hàng
nên A, G, I thẳng hàng

Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng

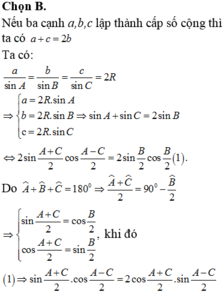


a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
=>\(AE\cdot AC=AF\cdot AB\)
b: Xét ΔADB vuông tại D có DM là đường cao
nên \(AM\cdot AB=AD^2\left(1\right)\)
Xét ΔADC vuông tại D có DN là đường cao
nên \(AN\cdot AC=AD^2\left(2\right)\)
Từ (1),(2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=>\(\dfrac{AN}{AM}=\dfrac{AE}{AF}\)
=>\(\dfrac{AE}{AN}=\dfrac{AF}{AM}\)
=>\(AN\cdot AF=AM\cdot AE\)
c: Xét ΔANM có \(\dfrac{AE}{AN}=\dfrac{AF}{AM}\)
nên EF//MN