Bài 3 (3 điểm ): Cho ∆ABC nhọn có trung tuyến AD. Gọi M là điểm thuộc tia AD sao cho D là trung điểm của AM.
a) Chứng minh AADC = AMDB. Từ đó suy ra BM//AC.
b) Gọi N là trung điểm của AC. Đường thẳng ND cắt MB tại K. Chứng minh D là trung điểm của KN.
c) Gọi I, E lần lượt là trung điểm của AK và AB. Chứng minh ba đường thẳng AD, CE, NI đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 8 2021
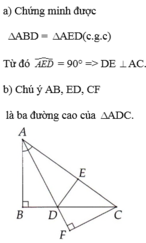
a: Xét ΔBFC và ΔCEB có
BF=CE
\(\widehat{FBC}=\widehat{ECB}\)
BC chung
Do đó: ΔBFC=ΔCEB
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
Ta có: ΔBFC=ΔCEB
nên \(\widehat{BFC}=\widehat{CEB}\)
mà \(\widehat{CEB}=90^0\)
nên \(\widehat{BFC}=90^0\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
CF là đường cao ứng với cạnh AB
Do đó: AM,BE,CF đồng quy
30 tháng 8 2021
a) Xét tam giác BFC và CEB ta có:
Góc FBC = góc ECB
BF = CE
BC cạnh chung
=> tam giác BFC = tam giác CEB (c-g-c)
30 tháng 8 2021
a: Xét ΔBFC và ΔCEB có
BF=CE
\(\widehat{FBC}=\widehat{ECB}\)
BC chung
Do đó: ΔBFC=ΔCEB
b: Ta có: ΔBFC=ΔCEB
nên \(\widehat{BFC}=\widehat{CEB}\)
mà \(\widehat{CEB}=90^0\)
nên \(\widehat{BFC}=90^0\)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
Xét ΔBAC có
AM là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
CF là đường cao ứng với cạnh AB
Do đó: AM,BE,CF đồng quy
30 tháng 8 2021
a: Xét ΔBFC và ΔCEB có
BF=CE
\(\widehat{FBC}=\widehat{ECB}\)
BC chung
Do đó: ΔBFC=ΔCEB
b: Ta có: ΔBFC=ΔCEB
nên \(\widehat{BFC}=\widehat{CEB}\)
mà \(\widehat{CEB}=90^0\)
nên \(\widehat{BFC}=90^0\)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AM là đường cao ứng với cạnh BC
Xét ΔBAC có
AM là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
CF là đường cao ứng với cạnh AB
Do đó: AM,BE,CF đồng quy
28 tháng 3 2023
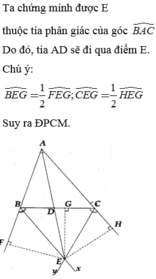
a: ΔABC can tại A
mà AD là trung tuyến
nên AD là phân giác
b: Xet ΔABE và ΔACF có
AB=AC
góc BAE chung
AE=AF
=>ΔABE=ΔACF
=>góc ABE=góc ACF=1/2*góc ABC
=>BE là phân giác của góc ABC
c: Xet ΔABC có
BE,CF,AD là phân giác
=>BE,CF,AD đồng quy
15 tháng 8 2019
Câu hỏi của ✎﹏ Ƈøｏȴ _ Ǥɩ®ʆ _☜♥☞ ✓ - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo nhé!
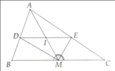
a: Xét ΔDAC và ΔDMB có
DA=DM
\(\widehat{ADC}=\widehat{MDB}\)(hai góc đối đỉnh)
DC=DB
Do đó: ΔDAC=ΔDMB
=>\(\widehat{DCA}=\widehat{DBM}\)
=>CA//BM
b: Xét ΔDNC và ΔDKB có
\(\widehat{DCN}=\widehat{DBK}\)
DC=DB
\(\widehat{NDC}=\widehat{KDB}\)(hai góc đối đỉnh)
Do đó: ΔDNC=ΔDKB
=>DN=DK
=>D là trung điểm của NK