Cho tam giác ABC và đường thẳng d // BC cắt AB và AC tại M và N thỏa mãn AM = CN. Biết M(- 4 ; 0) ; C (5 ; 2). Chân đường phân giác trong góc A là D (0 ; -1). Tìm tọa độ hai điểm A và B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm

a) Xét ΔABC có
MN//BC(gt)
Do đó: \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)(Định lí Ta lét)
Suy ra: \(\dfrac{6}{4}=\dfrac{8}{NC}\)
hay \(NC=\dfrac{16}{3}cm\)
Ta có: AM+MB=AB(M nằm giữa A và B)
nên AB=6+4=10(cm)
Ta có: AN+NC=AC(N nằm giữa A và C)
nên \(AC=8+\dfrac{16}{3}=\dfrac{40}{3}cm\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{40}{3}\right)^2=\dfrac{2500}{9}\)
hay \(BC=\dfrac{50}{3}cm\)
Xét ΔABC có
MN//BC(gt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{MN}{\dfrac{50}{3}}=\dfrac{6}{10}\)
\(\Leftrightarrow MN=\dfrac{6\cdot\dfrac{50}{3}}{10}=\dfrac{100}{10}=10cm\)
Vậy: MN=10cm; \(NC=\dfrac{16}{3}cm\); \(BC=\dfrac{50}{3}cm\)

A B C D E M N F
Qua D kẻ đường thẳng song song với AC và nó cắt cạnh AB ở F.
Ta có: DM//AB hay DM//AF. Mà DF//AC hay DF//AM => DM=AF và DF=AM (T/c đoạn chắn)
DF//AC => ^FDB=^NCE (Đồng vị); BF//EN =>^FBD=^NEC (Đồng vị)
Xét tam giác BFD và tam giác ENC có:
^FDB=^NCE
DB=EC => Tam giác BFD=Tam giác ENC (g.c.g)
^FBD=^NEC
=> DF=CN (2 cạnh tương ứng) . Mà DF=AM (cmt) => AM=CN (đpcm)

Điểm M nằm giữa A và B nên: AB = AM + MB = 4 + 8 = 12cm
Áp dụng hệ quả định lí Ta let ta có;
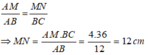
Chọn đáp án C